Introdução à teoria pós-tonal (4a. ed.).
3. Algumas propriedades e relações adicionais.
3.1 Notas comuns sob transposição (Tn).
Quando um conjunto de classes de notas é transposto ou invertido, o seu conteúdo mudará inteiramente, parcialmente ou, não mudará. Notas mantidas em comum entre dois membros diferentes da mesma classe de conjuntos podem produzir uma continuidade musical importante. Ao contrário, a ausência de notas comuns pode enfatizar o contraste entre dois membros diferentes da mesma classe de conjuntos.
3.1.1 Conteúdo classe-intervalar.
Quando se transpõe um conjunto de classes de notas pelo intervalo n, a quantidade de notas comuns igualará a quantidade de vezes que o intervalo n ocorre no conjunto (com uma exceção a ser discutida mais adiante). A escala maior contém seis instâncias da classe de intervalos 5, assim, haverá seis notas comuns quando a escala for transposta por cinco semitons mais agudos ou mais graves (T5 ou T7).

Para entender por que isso acontece, rastreia-se os mapeamentos envolvidos. Quando um conjunto é transposto à Tn, cada membro do conjunto mapeia-se em uma nota que estará n semitons mais aguda. Se duas das notas do conjunto estiverem separadas por n semitons, transpô-las por n semitons mapeará uma das notas na outra, produzindo uma nota comum. Esse mapeamento ocorrerá tantas vezes quantas forem as ocorrências do intervalo n no conjunto. Em outras palavras, para cada ocorrência de um dado intervalo n, haverá uma nota comum sob Tn (novamente, com uma exceção a ser discutida mais adiante).
Por exemplo, aplicar T3 a [4, 5, 7, 8], um membro da cc(0134). Há duas ocorrências da classe de intervalos 3 no conjunto: entre 4 e 7 e entre 5 e 8. Como resultado, quando o conjunto for transposto três semitons mais agudo (T3), o 4 mapear-se-á no 7 e o 5 mapear-se-á no 8. Semelhantemente, quando ele for transposto três semitons mais grave (T9), o 8 mapear-se-á no 5 e o 5 mapear-se-á no 4. Ver o Exemplo 3-2.
![T3 aplicada a [4, 5, 7, 8] produz duas notas em comum](tpt_3/ex_ncst_2.png)
![Um único trítono em [4, 9, 10] produz duas notas em comum à T6](tpt_3/ex_ncst_tt.png)
Para descobrir quantas notas em comum um conjunto terá em qualquer nível de transposição, simplesmente olha-se o seu vetor classe-intervalar. O vetor diz quantas vezes cada classe de intervalos ocorre em qualquer conjunto, o que também diz quantas notas em comum haverá sob Tn para qualquer valor de n. Por exemplo, (0145)[*] tem o vetor classe-intervalar [201210] e, portanto, manterá duas notas em comum à T1 (ou T11) e T4 (ou T8) e, uma única nota em comum à T3 (ou T9 e T5 (ou T7). Não manterá notas em comum à T2, T6 ou T10. Esses resultados manter-se-ão para todos os membros da classe de conjuntos.
Ver no Exemplo 3-4 ao lado como criar uma cadeia de cc(0145), conectadas por notas em comum.
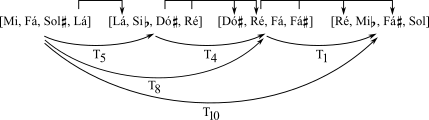
O Exemplo 3-5 a seguir mostra os mapeamentos utilizados no Exemplo 3-4. As transposições à T5 e T8 produzem uma única nota em comum, enquanto as transposições à T4 e T1 produzem duas notas em comum cada. O movimento geral T10 não produz notas em comum porque no conjunto sendo transposto não contém ci10 (ou ci2).
3.1.2 Algumas classes de conjuntos especiais.
O vetor classe-intervalar da escala maior é [254361]. Ele tem uma quantidade diferente de ocorrências de cada classe de intervalos. Como resultado, haverá uma quantidade diferente de notas em comum para cada nível de transposição (exceto para o semitom e para o trítono, onde haverá duas notas em comum, ver a Figura 3-1). Devido a essa propriedade (chamada multiplicidade exclusiva de classes de intervalos) , a escala maior (e a escala menor natural, um membro da mesma classe de conjuntos) pode criar a hierarquia de tonalidades vizinhas e afastadas que é tão essencial para a música tonal.

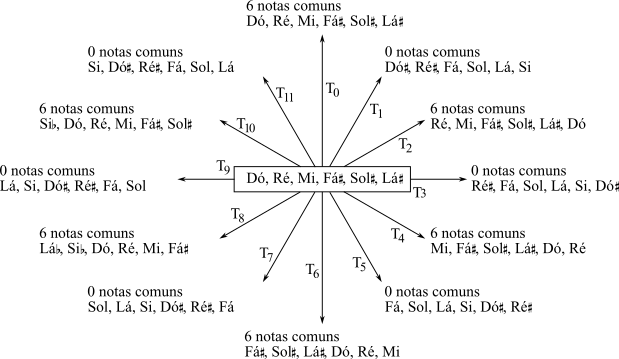
Em contraste, observe-se o vetor classe-intervalar da escala de tons inteiros: [060603]. Para cada nível de transposição par (T0, T2, T4, T6, T8, T10), haverá seis notas comuns (isto é, a duplicação da escala original); para cada nível de transposição ímpar (T1, T3, T5, T7, T9, T11),não haverá nenhuma (ver a Figura 3-2). Não há uma gradação contínua de valores, apenas um rígido tudo ou nada.
Uma observação final sobre notas em comum sob transposição: para qualquer conjunto transposto à T0 haverá tantas notas em comum quantas forem as notas do conjunto (i.e., o conteúdo das cn não mudará). Isso acontece porque cada cn do conjunto forma o intervalo 0 (uníssono) consigo mesmo.
Quando um conjunto é transposto à Tn, a quantidade de notas em comum será igual à quantidade de ocorrências de n no conjunto (exceto para T6, a transposição do trítono, que será o dobro daquela quantidade.
3.2 Simetria por transposição.
Uma pequena quantidade de conjuntos, como a escala de tons inteiros, é capaz de mapear-se inteiramente em si mesmos sob transposição (a qualquer nível diferente de T0). Conjuntos com essa capacidade são ditos simétricos por transposição.
3.2.1 Vetor Classe-intervalar.
Se o vetor classe-intervalar contém uma entrada igual à quantidade de notas do conjunto (ou metade daquela quantidade no caso do trítono), então o conjunto tem esta propriedade. O Quadro 3-1 a seguir lista todas as classes de conjuntos simétricos por inversão junto com seus vetores classe-intervalares e seus níveis de simetria transpositiva.
Quadro 3-1: as quatorze classes de conjuntos simétricos-Tn.
| Classe de conjuntos Nome de Forte (forma prima) | Nome familiar | Modo de Messiaen | Vetor ci | Níveis de simetria-Tn | Graus de simetria-Tn |
|---|---|---|---|---|---|
| 2-6 (06) | Trítono | [000001] | T0, T6 | 2 | |
| 3-12 (048) | Tríade aumentada | [000300] | T0, T4, T8 | 3 | |
| 4-9 (0167) | [200022] | T0, T6 | 2 | ||
| 4-25 (0268) | Acorde de sexta aumentada francesa | [020202] | T0, T6 | 2 | |
| 4-28 (0369) | Acorde de sétima diminuta | [004002] | T0, T3, T6, T9 | 4 | |
| 6-7 (012678) | Modo 5 | [420243] | T0, T6 | 2 | |
| 6-30 (013679) | Acorde de "Petrushka" | [224223] | T0, T6 | 2 | |
| 6-20 (014589) | Escala hexatônica | [303630] | T0, T4, T8 | 3 | |
| 6-35 (02468A) | Escala de tons inteiros | Modo 1 | [060603] | T0, T2, T4, T6, T8, T10 | 6 |
| 8-9 (01236789) | Modo 4 | [644464] | T0, T6 | 2 | |
| 8-25 (0124678A) | Modo 6 | [464644] | T0, T6 | 2 | |
| 8-28 (0134679A) | Escala octatônica | Modo 2 | [448444] | T0, T3, T6, T9 | 4 |
| 9-12 (01245689A) | Escala eneatônica (nonatônica) | Modo 3 | [666963] | T0, T4, T8 | 3 |
| 10-6 (012346789A) | Modo 7 | [888885] | T0, T6 | 2 |
3.2.2 Algumas classes de conjuntos especiais.
Evidentemente essa propriedade interessou os compositores, pois muitas dessas classes de conjuntos são familiares, incluindo a tríade aumentada, o acorde de sexta aumentada francesa, o acorde de sétima diminuta, o acorde de "Petroushka", a escala hexatônica, a escala de tons inteiros e a escala octatônica.
O compositor francês Oliver Messiaen esteve extremamente interessado nessas classes de conjuntos como recurso compositivo. Ele identificou sete delas como "Modos de transposição limitada", conforme estão indicados na terceira coluna do Quadro anterior e as usou extensivamente em sua música.
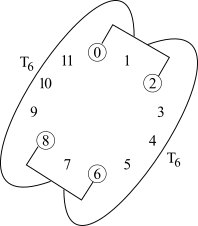
No Exemplo 3-6 ao lado há duas instâncias de acordes de sexta aumentada francesa transpostos à T6. Nesse nível de transposição (0268) mapeia-se em si mesmo de modo que se obtém as mesmas quatro notas nas duas instâncias. [Há outras transposições que mantém duas notas em comum: T2 e T4.] O nível das notas muda, mas o conteúdo das classes intervalares permanece o mesmo — esse é o efeito da simetria por transposição. [*]
3.2.3 O mostrador de relógio de classes de notas.
Das muitas relações discutidas, a simetria transpositiva é talvez a mais fácil de visualizar no mostrador de relógio de classes de notas. Na Figura 3-3 a seguir vê-se [0, 2, 6, 8] disposto no mostrador de relógio. A mesma torção de seis semitons no sentido horário que move [0, 2] para [6, 8] simultaneamente move [6, 8] para [0, 2]. O conjunto está configurado de modo que se pode girá-lo no mostrador de relógio até que ele se encaixe de volta nele mesmo. De fato, isso que se está chamando de simetria transpositiva, os matemáticos chamam de simetria rotativa.
3.2.4 Graus de simetria transpositiva.
Ao olhar-se a coluna do meio na Lista de classes de conjuntos, o número antes da vírgula mede o grau de simetria transpositiva, isso é, a quantidade de níveis de transposição aos quais a classe ou as classes de conjuntos naquela linha da lista mapear-se-ão nelas mesmas. O número é pelo menos 1, porque todo conjunto mapeia-se em si mesmo à T0 e assim é transpositivamente simétrico ao menos nesse sentido trivial. As quatorze classes de conjuntos listadas no Quadro 3a são aquelas com um grau de simetria transpositiva maior do que 1.
Um conjunto é transpositivamente simétrico se ele se mapeia nele mesmo sob transposição (outra além da trivial T0).
3.3 Notas comuns sob Inversão (In).
Quando se discute notas comuns sob Tn leva-se em conta os intervalos (diferenças) formados por cada par de notas do conjunto. Agora, ao discutir notas comuns sob In, leva-se em conta os números de índice (somas) formados por cada par de notas do conjunto. A soma de qualquer par de notas será o número de índice n tal que In mapeia aquelas notas uma na outra.
3.3.1 Calculando notas comuns sob inversão.
Por exemplo, considere-se [1, 3, 6, 9], um membro da cc(0258). No Quadro 3-2 a seguir, estão calculadas todas as somas possíveis. Cada soma n produzida por duas notas diferentes resulta em duas notas comuns sob In, já que aquelas duas notas se mapeiam uma na outra. Cada soma n produzida pela adição de uma nota consigo mesma resulta em uma nota comum sob In, já que aquela nota se mapeia nela mesma (Quadro 3-2).
Quadro 3-2: notas comuns sob inversão para [1, 3, 6, 9]
| [1, 3, 6, 9] | |
|---|---|
| 1 + 3 = 4 | 1 e 3 são notas comuns sob I4: [7, 10, 1, 3] |
| 1 + 6 = 7 | 1 e 6 são notas comuns sob I7: [10, 1, 4, 6] |
| 1 + 9 = 10 | 1 e 9 são notas comuns sob I10: [1, 4, 7, 9] |
| 3 + 6 = 9 | 3 e 6 são notas comuns sob I9: [0, 3, 6, 8] |
| 3 + 9 = 0 | 3 e 9 são notas comuns sob I0: [3, 6, 9, 0] |
| 6 + 9 = 3 | 6 e 9 são notas comuns sob I3: [6, 9, 0, 2] |
| 1 + 1 = 2 | 1 é uma nota comum sob I2: [5, 8, 11, 1] |
| 3 + 3 = 6 | 3 é uma nota comum sob I6: [9, 0, 3, 5] |
| 6 + 6 = 0 | 6 é uma nota comum sob I0: [3, 6, 9, 11] |
| 9 + 9 = 6 | 9 é uma nota comum sob I6: [9, 0, 3, 5] |
Um jeito simples de descobrir a quantidade de notas comuns sob In, é construir uma tabela de adição, com um conjunto escrito ao longo dos eixos vertical e horizontal e as somas preenchendo as linhas e colunas da tabela. Uma tabela de adição desse tipo para [3, 4, 7, 8] está no Exemplo 3-7.
![usando uma tabela de adição para encontrar notas comuns sob inversão para [3, 4, 7, 8]](tpt_3/tab_ad.png)
Essa tabela ordenadamente executa todas as adições requeridas: ela adiciona cada nota duas vezes com cada uma das outras e uma vez consigo mesma. Como resultado, cada ocorrência de um número dentro da tabela representa uma única nota em comum. O número 11 ocorre quatro vezes, portanto, haverá quatro notas em comum à I11; o número 3 ocorre duas vezes, portanto, haverá duas notas em comum à I3.
Essa tabela de adição tem outra vantagem: ela mostra não apenas quantas notas serão mantidas em comum sob In, mas também quais. Cada número de índice na tabela posiciona-se na interseção de duas notas. Aquelas serão as notas mapeadas uma na outra por aquele número de índice. Por exemplo, 10 ocorre na interseção de 3 e 7, 3 e 7 são assim mantidos à I10. Semelhantemente, 8 ocorre na interseção de 4 consigo mesmo, assim 4 será mantido em comum à I8.
3.3.2 Notas comuns como fonte de continuidade musical.
Notas comuns sob transposição e inversão podem ser uma fonte importante de continuidade musical. O Exemplo 3-7 ao lado faz uso intensivo ds cc(0148). [O exemplo de Straus é diferente.] Há 4 instâncias da cc(0148) na melodia da clarineta. O vetor classe intervalar é [101310]. As transposições usadas são: T9 que mantém uma nota em comum, T6 que não mantêm notas em comum e, T4 que mantém 3 notas em comum. As inversões usadas vão gradualmente tendo notas a menos em comum: I0 têm 3 notas em comum, I1 tem duas notas em comum, I2 tem uma e I3 nenhuma. Observe que T9 e I3 tem as mesmas notas.
Quando um conjunto é invertido à In, haverá duas notas em comum para cada soma n formada pela adição das classes de notas umas com as outras e, uma nota em comum para cada soma n formada pela adição das classes de notas com elas mesmas.
3.4 Simetria inversiva.
Algumas classes de conjuntos contêm conjuntos que podem mapear-se inteiramente neles mesmos sob inversão. Tais classes de conjuntos são ditas inversivamente simétricas. Das 232 classes de conjuntos na Lista de classes de conjuntos, 79 têm essa propriedade (as díades e decacordes, os quais são todos inversivamente simétricos, estão excluídos dessa contagem).
3.4.1 Palíndromo intervalar (imagem espelhada).
Conjuntos que são inversivamente simétricos podem ser escritos de modo que lendo-se os intervalos da esquerda para a direita sejam os mesmos lendo-se da direita para a esquerda. Esse palíndromo intervalar geralmente estará presente quando o conjunto estiver escrito em forma normal, embora ocasionalmente uma nota tenha que ser escrita duas vezes para capturar a circuição modular (ver o Exemplo 3-9).

O senso de conjuntos simetricamente inversivos como sua própria imagem espelhada é ainda mais aparente quando eles estão escritos em torno do mostrador de relógio de classes de notas (Figura 3-4). Em conjuntos simetricamente inversivos, todas as notas do conjunto mapeiam-se em outras notas ou nelas mesmas sob alguma In. Cada nota do conjunto tem um parceiro inversivo que está também no conjunto.

3.4.2 Simetria de notas e simetria de classes de notas.
O Exemplo 3-10 mostra um pentacorde simetricamente inversivo no mostrador de relógio de classes de notas.

A simetria deve estar aparente - cada nota do acorde tem um parceiro inversivo que está também no acorde e o Mi equilibra-se como um centro de simetria. Seria fácil escrever este acorde ou qualquer outro acorde simetricamente inversivo de modo a perceber a sua simetria no espaço de notas: os três acordes do Exemplo 3-10(b) dispõem aquelas cinco classes de notas de modo que elas descrevem os mesmos intervalos de notas lendo-se de baixo para cima bem como de cima para baixo. Esses três acordes são nota-simétricos ‒ eles são simétricos em registro e seus intervalos de notas formam um palíndromo. Qualquer conjunto de classes de notas simpetrico pode ser disposto simetricamente no espaço de notas.
Mas não foi assim que Schoenberg o escreveu no início da sua Peças para orquestra, op. 16, no. 3 ("Farben"). O acorde real escrito no Exemplo 3-10(c) é classe-de-nota-simétrico, mas não nota-simétrico. A simetria inversiva ainda está ali ‒ cada nota do acorde tem seu parceiro inversivo que está também no acorde ‒ mas ela é sentida apenas no mais abstrato espaço de notas, não no mais concreto e imediato espaço de notas.
Enquanto a simetria inversiva é em geral uma importante fonte compositiva, ela pode desempenhar um papel particularmente decisivo quando a simetria é percebida no espaço de notas. Qualquer membro da cc(012), por exemplo, é abstratamente simétrico (i.e., simétrico no espaço de classes de notas) não importa como ele esteja disposto, mas a sua simetria pode ser drasticamente reforçada pela arrumação das notas nos registros.
3.4.3 Graus de simetria inversiva.
Assim como as classes de conjuntos que são transpositivamente simétricas, as que são inversivamente simétricas podem ser facilmente identificadas na Lista de classes de conjuntos. Na coluna do meio, o número após a vírgula mede o grau de simetria inversiva ‒ ele diz a quantidade de níveis inversivos aos quais um conjunto mapeia-se nele mesmo. Muitos conjuntos não podem mapear-se em si mesmos sob inversão e, portanto, tem um grau de simetria inversiva de 0. Alguns conjuntos podem mapear-se em si mesmos em um ou mais de um nível de inversão. A cc(024), por exemplo, tem um grau de simetria de (1, 1). ela mapeia-se em si mesma em um nível transpositivo (T0) e um nível inversivo (I4). O conjunto mais simétrico de todos é a escala de tons inteiros; ela mapeia-se nela mesma em seis níveis transpositivos e seis inversivos: seu grau de simetria é (6, 6).
A simetria transpositiva é uma propriedade razoavelmente comum, mas a simetria inversiva em mais de um nível é rara - somente as onze classes de conjuntos listadas no quadro 3-3 a tem.
Quadro 3-3: Onze classes de conjuntos com grau de simetria inversiva maior do que 1.
| Classe de conjuntos | Nome familiar | Níveis de simetria-In | Grau de simetria-In |
|---|---|---|---|
| 3-12 (048) | Tríade aumentada | I0, I4, I8 | 3 |
| 4-9 (0167) | I1, I7 | 2 | |
| 4-25 (0268) | Acorde de sexta aumentada francesa | I2, I8 | 2 |
| 4-28 (0369) | Acorde de sétima diminuta | I0, I3, I6, I9 | 4 |
| 6-7 (012678) | I2, I8 | 2 | |
| 6-20 (014589) | Escala hexatônica | I1, I5, I9 | 3 |
| 6-35 (02468A) | Escala de tons inteiros | I0, I2, I4, I6, I8, I10 | 6 |
| 8-9 (01236789) | I3, I9 | 2 | |
| 8-25 (0124678A) | I2, I8 | 2 | |
| 8-28 (0134679A) | Escala octatônica | I1, I4, I7, I10 | 4 |
| 9-12 (01245689A) | Escala eneatônica (nonatônica) | I2, I6, I10 | 3 |
É interessante comparar esta lista com a lista de classes de conjuntos que são transpositivamente simétricas no Quadro 3a. Virtualmente todas as classes de conjuntos que são transpositivamente simétricas também são inversivamente simétricas em mais de um nível [(013679) é a única exceção], e todas as classes de conjuntos que são inversivamente simétricas em mais de um nível também são transpositivamente simétricas. E, como observado anteriormente, as classes de conjuntos com uma ou ambas as propriedades geralmente têm se provado atrativas para os compositores, incluindo a tríade aumentada (048), o acorde de sétima diminuta (0369) e, a escala hexatônica (014589), a escala de tons inteiros (02468A) e, as escalas octatônicas (0134679A).
Um conjunto é inversivamente simétrico se ele se mapeia em si mesmo sob inversão. Tais conjuntos podem ser escritos como palíndromos, com os mesmos intervalos de baixo para cima e de cima para baixo.
3.5 Simetria e classes de conjuntos.
Quanto mais simétrico for o conjunto (i.e., quanto maior for a quantidade de operações que mapeiam um conjunto nele mesmo), menor será a quantidade de conjuntos distintos na classe de conjuntos. Muitas classes de conjuntos têm um grau de simetria de (1, 0) e contém vinte e quatro conjuntos distintos. Para todas as classes de conjuntos, dividir 24 pela quantidade de operações automapeadoras dará a quantidade de conjuntos na classe de conjuntos. A classe de conjuntos (0167), por exemplo, tem um grau de simetria de (2, 2). Isso significa que cada conjunto na classe de conjuntos mapear-se-á em si mesmo de quatro maneiras: duas Tn e duas In. O Quadro 3-4 mostra os seis membros da cc(0167) e as quatro transformações (duas T e duas I) que irão produzi-las (assumindo que [0, 1, 6, 7] seja designado como T0).
Quadro 3-4: os seis conjuntos que são membros da cc(0167).
| [0, 1, 6, 7] | T0, T6, I1, I7 |
| [1, 2, 7, 8] | T1, T7, I2, I8 |
| [2, 3, 8, 9] | T2, T8, I3, I9 |
| [3, 4, 9, 10] | T3, T9, I4, I10 |
| [4, 5, 10, 11] | T4, T10, I5, I11 |
| [5, 6, 11, 0] | T5, T11, I6, I0 |
Para usar um exemplo mais familiar da mesma coisa, há somente três acordes de sétima diminuta. Isso porque há oito transformações (quatro T e quatro I) que mapeiam qualquer membro de (0369) nele mesmo e, 24 dividido por 8 é 3.
O tamanho de uma classe de conjuntos irá variar de acordo com o grau de simetria transpositiva e inversiva.
3.6 Relação-Z.
Quaisquer dois conjuntos relacionados por transposição ou inversão têm o mesmo conteúdo classe-intervalar. O contrário, entretanto, não é verdadeiro. Há muitos pares de conjuntos (um par de tetracordes, três pares de pentacordes e quinze pares de hexacordes) que têm o mesmo conteúdo classe-intervalar, mas não são relacionados uns com os outros nem por transposição nem por inversão e, portanto, não são membros da mesma classe de conjuntos. Conjuntos que têm o mesmo conteúdo classe-intervalar, mas não são transposições ou inversões um do outro são chamados conjuntos Z-relacionados e a relação entre eles é a relação-Z. (O Z significa "zigótico".) Conjuntos com a relação-Z soarão muito semelhantes porque eles têm o mesmo conteúdo classe-intervalar, mas não estarão tão proximamente relacionados uns com os outros como os conjuntos que são membros da mesma classe de conjuntos. [Ver o Exemplo 3-11 ao lado. Não há exemplo em Straus.]
3.6.1 Z-correspondentes.
A relação Z é um caso em que os "nomes de Forte" são úteis. Qualquer classe de conjuntos com um Z no seu nome de Forte tem uma Z-correspondente, outra classe de conjuntos com uma forma prima diferente, mas com o mesmo vetor classe-intervalar. Na Lista de classes de conjuntos, os hexacordes Z-relacionados estão listados um ao lado oposto do outro, e o seu vetor classe-intervalar compartilhado está entre eles. Para conjuntos de outros tamanhos, ter-se-á que procurar na lista para encontrar as duas classes de conjuntos que têm o mesmo vetor classe-intervalar.
3.6.2 Os dois tetracordes "todos-intervalos".
Os compositores têm se interessado nos dois tetracordes "todos-intervalos": 4-Z15 (0146) e 4-Z29 (0137). Eles são chamados de tetracordes todos-intervalos porque, como sugere o seu vetor classe-intervalar compartilhado, [111111], ambos os tetracordes contém uma ocorrência de cada uma das classes de intervalos. Ver o Exemplo 3-12 a seguir. [O Exemplo de Straus é diferente.]
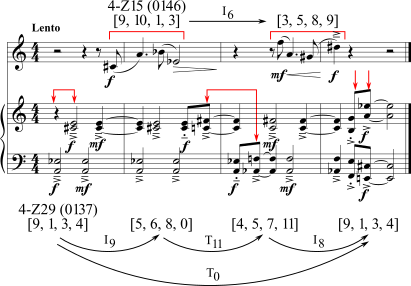
Dois conjuntos são Z-relacionados se eles têm o mesmo conteúdo classe-intervalar, mas não são relacionados por T ou I.
3.7 Relação de complemento.
Para qualquer conjunto, as classes de notas excluídas constituem o seu complemento. O complemento de [2, 3, 6, 9], por exemplo, é [4, 5, 7, 8, 10, 11, 0, 1]. Qualquer conjunto e seu complemento tomados juntos, conterão todas as doze classes de notas. Para qualquer conjunto contendo n notas, o seu complemento conterá 12 - n notas.
3.7.1 Conteúdo intervalar.
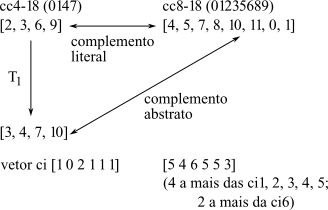
Há uma importante semelhança intervalar entre um conjunto e o seu complemento. Pode-se pensar que, quaisquer intervalos que um conjunto tenha muitos, o seu complemento terá poucos e vice-versa. Acontece, entretanto, que um conjunto e seu complemento sempre têm uma distribuição surpreendentemente semelhante de intervalos. Para os conjuntos complementares, a diferença na quantidade de ocorrências de cada intervalo é igual à diferença entre o tamanho dos conjuntos (exceto para a quantidade de trítonos, que será metade da diferença entre os tamanhos dos conjuntos). Considerando os conjuntos do Exemplo 3-13 como um exemplo, o primeiro conjunto tem o vetor classe-intervalar [102111]; o seu complemento tem o vetor classe intervalar [546553]. O conjunto de oito notas tem quatro a mais de tudo (exceto pelo trítono, ci6, do qual ele dois a mais). O conjunto maior é como uma versão expandida do seu complemento menor.

Os nomes de Forte para as classes de conjuntos são projetados para identificar a relação de complemento. Se os números antes do traço somam 12 e, se os números após o traço são os mesmos (como por exemplo, 4-18 e 8-18 no exemplo anterior), as duas classes de conjuntos são complemento-relacionadas. Os nomes de Forte serão assim úteis ao se falar sobre a relação de complemento.
A relação de complemento é particularmente importante em muitas músicas nas quais as doze classes de notas estão circulando relativamente livres e nas quais o agregado (uma coleção contendo todas as doze classes de notas) é uma importante unidade estrutural. Considere-se o Exemplo 3-14 ao lado.
3.7.2 Complementos literais e abstratos.
Porque o conteúdo intervalar não é modificado por transposição ou inversão, a estreita semelhança intervalar dos conjuntos complementares permanece verdadeira mesmo quando os conjuntos são transpostos ou invertidos. Assim, mesmo se os conjuntos não forem literalmente complementares (i.e., um exclui as notas do outro), as relações intervalares perduram conquanto os conjuntos sejam abstratamente complementares, (i.e., membros de classes de conjuntos complemento-relacionadas). Novamente com referência aos conjuntos do Exemplo 3-13, ao transpor o primeiro conjunto à T1, o conjunto de quatro notas não será mais o complemento literal do conjunto de oito notas: de fato, eles agora compartilham três notas em comum (Exemplo 3-15 a seguir). Entretanto, eles são membros de classes de conjuntos complemento-relacionadas e, portanto, tem uma distribuição semelhante de intervalos. Conjuntos complemento-relacionados não têm tanto em comum quanto conjuntos transpositiva ou inversivamente relacionados, mas eles têm uma sonoridade similar por causa da similaridade do seu conteúdo classe intervalar.
3.7.3 Lista de Classes de Conjuntos.
A Lista de classes de conjuntos está arranjada para ver facilmente a relação de complemento. Há a mesma quantidade de classes de díades e de decacordes (6), de classes de tricordes e nonacordes (12), de classes de tetracordes e octacordes (29) e, de classes de pentacordes e septacordes (38) (hexacordes serão discutidos mais adiante.) As classes de conjuntos complementares estão sempre listadas na mesma linha, uma ao lado oposto da outra. Ao procurar-se 4-19 (0148) e 8-19 (01245689), ver-se-á que é assim. Conforme observado previamente, os nomes de Forte de conjuntos complementares sempre têm o mesmo número seguindo o traço. Logo, 4-19 e 8-19 são complementos um do outro, bem como o são 3-6 e 9-6, 5-Z12 e 7-Z12 e assim por diante.
Essas características da lista facilitam encontrar conjuntos maiores. Considere-se um conjunto de nove notas que se quer encontrar na lista. Pode-se colocá-lo em forma prima e procurar , mas essa seria uma operação demorada, já que o conjunto é tão grande. É muito mais fácil pegar as três notas excluídas do conjunto de nove notas e então colocá-las em forma prima e depois procurar o tricorde na lista ‒ a forma prima do conjunto original de nove notas estará diretamente ao lado.
Classes de conjuntos complementares têm afinidades que extrapolam a sua distribuição intervalar similar. Classes de conjuntos complemento-relacionadas sempre tem o mesmo grau de simetria e, portanto, a mesma quantidade de conjuntos na classe. Classes de conjuntos complemento-relacionadas compartilham a relação Z: se um Conjunto X é Z-relacionado com um Conjunto Y, então o complemento de X será Z-relacionado ao complemento de Y. Em cada uma dessas formas, os conjuntos e as classes de conjuntos assemelham-se aos seus complementos.
3.7.4 Hexacordes.
Pode-se observar na Lista de classes de conjuntos que alguns hexacordes não tem nada escrito ao seu lado oposto. Hexacordes como aqueles são autocomplementares ‒ eles e seus complementos são membros da mesma classe de conjuntos. Como um exemplo simples, considere-se o hexacorde [2, 3, 4, 5, 6, 7]. O seu complemento literal é [8, 9, 10, 11, 0, 1]. Mas ambos os conjuntos são membros da cc6-1 (012345). Em outras palavras, hexacordes autocomplementares são aqueles que podem se mapear em seus complementos ou por T ou por I.
Se um hexacorde não é autocomplementar, então ele deve ser Z-relacionado ao seu complemento. Observe-se que, com conjuntos complementares a diferença na quantidade de ocorrências de qualquer intervalo é igual à diferença de tamanho dos dois conjuntos. Mas um hexacorde tem exatamente o mesmo tamanho do seu complemento. Como resultado, um hexacorde sempre tem exatamente o mesmo conteúdo classe-intervalar do seu complemento. Se ele também é relacionado ao seu complemento por T ou I, então ele é autocomplementar. Se não, então ele é Z-relacionado com o seu complemento. Os hexacordes na lista estão assim escritos ou com nada do lado oposto ou, ao lado oposto de seus Z-correspondentes. A relação intervalar entre hexacordes complementares é extremamente importante para a música dodecafônica que será discutida em outras unidades.
A música do Exemplo 3-16 ao lado pode ser entendida em relação aos três hexacordes rotulados como X, Y e Z. [O exemplo musical de Straus é diferente, mas o texto pode ser aplicado ao exemplo em foco.]
X e Y são complementos literais um do outro: cada um contém as notas excluídas pelo outro e juntos criam um agregado de todas as doze classes de notas. Esses dois hexacordes não estão relacionados por T ou I e, portanto, não são membros da mesma classe de conjuntos. Mas, porque eles têm o mesmo conteúdo intervalar do seu complemento (como todos os hexacordes), eles são Z-relacionados. Z é uma transposição de Y à T7. Como resultado, X e Z não são mais literalmente complementos um do outro (de fato, eles compartilham quatro das seis notas). Mas por serem membros de classes de conjuntos complemento-relacionadas (i.e., eles são complementos abstratos um do outro), eles ainda têm o mesmo conteúdo intervalar.
Dois conjuntos são complementos literais se eles não têm classes de notas em comum e juntos contém todas as doze classes de notas. Os conjuntos são complementos abstratos se eles pertencem a classes de conjuntos complemento-relacionadas.
3.8 Relação de inclusão (subconjuntos e superconjuntos).
Se um Conjunto X está incluído num Conjunto Y, então X é um subconjunto de Y e Y é um superconjunto de X. Um conjunto que contenha n classes de notas conterá 2n (2 elevado à enésima potência) conjuntos. Um conjunto de quatro notas, por exemplo, conterá os seguintes subconjuntos: o conjunto nulo (um conjunto contendo nota nenhuma), 4 conjuntos de uma nota, 6 conjuntos de duas notas (também chamados díades ou intervalos), 4 conjuntos de três notas e, 1 conjunto de quatro notas (o próprio conjunto original). Isso perfaz um total de 24 ou seja, dezesseis conjuntos. O conjunto nulo, os conjuntos de uma nota e o próprio conjunto geralmente não serão de particular interesse como subconjuntos. Mesmo assim, restam muitos subconjuntos a serem considerados [2n - (n + 2)] e, naturalmente, quanto maior for o conjunto, mais numerosos serão os subconjuntos.
3.8.1 Subconjuntos do mesmo tipo.
A quantidade de possibilidades pode parecer opressiva, mas há duas coisas para se ter em mente. Primeiro alguns dos subconjuntos podem ser membros da mesma classe de conjuntos. A cc(0268), por exemplo, é um caso extremo. Todos os seus subconjuntos de três notas são membros da mesma classe de conjuntos, (026). Muitas classes de conjuntos não são tão restritas no seu conteúdo de subconjuntos como essa, mas geralmente há alguma redundância.
3.8.2 Malha de inclusão.
Para se ter uma imagem completa do conteúdo de subconjuntos de um conjunto, pode ser útil construir uma malha de inclusão que lista todas as classes de um dado conjunto bem como os subconjuntos daqueles subconjuntos. O Exemplo 3-17 contém uma malha de inclusão para a classe de conjuntos (014589), também conhecida como coleção hexatônica (a ser discutida em outra unidade). Todos os seis de seus subconjuntos de cinco notas são membros da cc(01458). Os cinco subconjuntos de quatro notas de (01458) por outro lado, representam quatro diferentes classes de tetracordes e eles contém algumas classes de tricordes como seus subconjuntos.

3.8.4 Projetando subconjuntos no espaço de notas.
[O Exemplo 3-18 ao lado aborda o tópico do exemplo de Straus que é diferente. O texto analítico ao lado, portanto, é diferente, ainda que similar. O texto que está aqui foi extraído do original no que pode ser aplicado genericamente.]
A segunda limitação importante no vasto mundo dos sub e superconjuntos é que somente uma pequena quantidade será musicalmente significativa em algum contexto musical específico. Como qualquer conjunto de seis notas, os acordes no Exemplo 3-18 (ao lado) contém muitos subconjuntos, mas apenas uma pequena quantidade deles pode ser ouvida como agrupamentos musicais significativos, identificados por registro compartilhado (ou articulados de alguma outra maneira). [...] Os subconjuntos de um conjunto são assim um tipo de potencial musical abstrato; o compositor escolhe quais enfatizar e quais reprimir.
3.8.5 Subconjuntos e superconjuntos literais e abstratos.
Assim como a relação de complemento, a relação de sub-superconjunto pode ser tanto literal quanto abstrata. O conjunto X é um subconjunto literal do conjunto Y se todas as notas de X estiverem contidas em Y. O conjunto X é um subconjunto abstrato do conjunto Y se qualquer forma transposta ou invertida de X estiver contida em Y, isto é, se qualquer membro de uma classe de conjuntos que contenha X for encontrada entre os subconjuntos de Y (Exemplo 3-19).
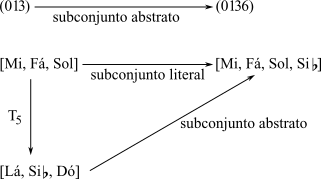
O conjunto [Mi, Fá, Sol] é um subconjunto literal de [Mi, Fá, Sol, Sib]. A transposição T5 de [Mi, Fá, Sol], [Lá, Sib, Dó], não é um subconjunto literal de [Mi, Fá, Sol, Sib]. Mas a classe de conjuntos que contém [Lá, Sib, Dó], nomeadamente (013), pode ser encontrada entre os subconjuntos literais de [Mi, Fá, Sol, Sib]. Assim, [Lá, Sib, Dó] é um subconjunto abstrato, não literal. de [Mi, Fá, Sol, Sib]. No mesmo sentido abstrato, pode-se dizer que a cc(013) é um subconjunto da cc(0136)
Tanto em sentido literal quanto abstrato, essas relações de inclusão são como a relação-Z e a relação de complemento, fontes potenciais de conexões musicais interessantes. Coleções menores podem frequentemente ser ouvidas combinando-se em outras maiores e coleções maiores dividindo-se em menores.
O Conjunto X é o subconjunto literal do Conjunto Y (e o Conjunto Y é o superconjunto literal do Conjunto X) se todas as classes de notas em X estão contidas em Y. O Conjunto X é o subconjunto abstrato do Conjunto Y (e o Conjunto Y é o superconjunto abstrato do Conjunto X) se alguma Tn(X) ou In(X) for um subconjunto literal de Y.
3.9 Combinação transpositiva (CT).
O processo de combinar pequenos conjuntos para formar outros maiores e dividir conjuntos grandes em outros pequenos é particularmente interessante quando os conjuntos menores combinados estão relacionados por inversão ou transposição. Já se viu anteriormente a simetria inversiva. Cada vez que se combina dois conjuntos da mesma classe que estão relacionados por inversão obtém-se um conjunto que é inversivamente simétrico. Por outro lado, qualquer conjunto inversivamente simétrico pode ser dividido em ao menos um par de subconjuntos simetricamente relacionados. A combinação transpositiva (CT) é a combinação de um conjunto com uma ou mais transposições de si mesmo para criar um conjunto maior. Do conjunto maior, o qual pode ser dividido em dois ou mais subconjuntos relacionados por transposição, diz-se ter a propriedade CT, e os conjuntos com essa propriedade geralmente provam-se de interesse para os compositores.
O Exemplo 3-20 [extraído da Sinfonia dos Salmos de Stravinsky] e esboçado de forma reduzida] inicia com uma ci3, Fá-Láb. Outra ci3, Mi-Sol, segue imediatamente um semitom mais grave. Aquela combinação de dois 3 separados por semitom é escrita como 3*1, onde o asterisco significa "transposto por". Pode-se também pensar em dois semitons (Mi-Fá e Sol-Láb) relacionados à T3, ou 1*3. De qualquer modo, a combinação de 1 e 3 produz uma forma da cc(0134). A mesma combinação produz um membro diferente da mesma classe de conjuntos, [Sib, Si, Dó#, Ré]. Esses dois tetracordes, criados por combinação transpositiva, são eles próprios combinados à T6 para criar um conjunto de oito notas. Pode-se sumariar o processo como: (3*1) * 6. Em outras palavras, um 3 é transposto por 1 e, o tetracorde resultante é transposto à T6. A passagem pode assim ser constituída de seus componentes menores pela combinação transpositiva.

O Quadro 3-5 lista todas as classes de tetracordes com a propriedade CT, juntamente com as díades (intervalos) que se combinam para criá-los e, dos quais elas podem ser desmembradas.
Quadro 3-5: propriedade CT para tetracordes.
| Tetracorde | Combinação transpositiva |
|---|---|
| (0123) | 1*2 |
| (0134) | 1*3 |
| (0145) | 1*4 |
| (0156) | 1*5 |
| (0167) | 1*6 e 5*6 |
| (0235) | 2*3 |
| (0246) | 2*4 |
| (0257) | 2*5 |
| (0268) | 2*6 e 4*6 |
| (0347) | 3*4 |
| (0358) | 3*5 |
| (0369) | 3*6 |
| (0158) | 4*5 |
Conjuntos podem ser combinados com suas próprias transposições para criar conjuntos maiores. Conjuntos com a propriedade CT podem ser divididos em subconjuntos transpositivamente relacionados.
3.10 Relações de contorno.
Até aqui o foco esteve em notas, classes de notas e seus intervalos. Explorou-se os meios pelos quais linhas e conjuntos de notas e classes de notas podem mover-se pelo e relacionar-se no espaço de notas e no espaço de classes de notas. Como ouvintes, às vezes pode ser mais fácil pensar no perfil geral da música, seus movimentos ascendentes e descendentes nos registros. Esses são aspectos do contorno musical. Para dar sentido ao contorno musical, não é necessário saber as notas e os intervalos exatos; precisa-se apenas saber quais notas são as mais agudas e quais são as mais graves.
3.10.1 Segmento de contorno (SEGC).
Compare-se os três fragmentos melódicos de quatro notas do Exemplo 3-21 ao lado. [O exemplo de Straus é diferente, mas o texto pode ser aplicado também a este.]
Embora os fragmentos contenham diferentes intervalos e representem diferentes classes de conjuntos, seus contornos são os mesmos. Cada um começa com a sua segunda nota mais aguda, continua com as suas notas mais grave e a segunda mais grave e, conclui com a sua nota mais aguda. No Exemplo 3-21 [ao lado], aquele contorno é representado como uma sequência de números dentro de colchetes angulares [sinais de menor do que e maior do que]: <2013>. As notas de cada fragmento recebem um número baseado na sua posição relativa no fragmento. A nota mais grave recebe o 0, a próxima mais grave recebe 1 e assim or diante. A nota mais aguda terá sempre um valor numérico que é 1 menos do que a quantidade de notas diferentes no fragmento. Os números são então distribuídos em ordem, para descrever o contorno musical. <2013> é o segmento de contorno ou SEGC e, aquela melodia intervalicamente variada é unificada, em parte, pelas três representações daquele único SEGC. Observe-se que agora se está falando de linhas (ou series), onde as coisas acontecem em uma ordem específica, não sobre coleções não ordenadas, como na discussão sobre conjuntos de classes de notas. Os colchetes angulares usados para designar SEGCs indicam que os elementos ocorrem numa ordem específica: <2013> diz que a segunda nota mais aguda vem primeiro, a nota mais grave vem depois, a segunda nota mais grave vem em terceiro e, a nota mais aguda vem por último.
3.10.2 Classes de SEGC.
[Novamente o exemplo de Straus é diferente, mas o texto aplica-se ao que está ao lado.] O Exemplo 3-21 [ao lado] tem uma versão variada da mesma melodia anterior. As notas são diferentes , mas o mesmo SEGC, <2013>, está representado quatro vezes. [No exemplo de Straus apenas três vezes.]
As notas são diferentes, mas o mesma SEGC, <2013>, está representado três vezes (Exemplo 3-21a) [na voz do soprano]. O SEGC criado pelas quatro notas começando em Mi* [na voz do contralto] é <1320> (Exemplo 3-21b). <2013> e <1320> estão relacionados por inversão. A nota mais aguda de um é substituída pela nota mais grave do outro, a segunda mais aguda pela segunda mais grave e assim por diante. Eles são imagens espelhadas um do outro. E assim como se compara duas linhas (ou séries) de classes de notas, os números na ordem de posição correspondente sempre perfazem a mesma soma, nesse caso 3. Um SEGC adicional, <0231>, ocorre duplamente (Exemplo 3-21c) [na voz do tenor]. <0231> e <2013> são retrógrado-relacionados ‒ cada um é o mesmo que o outro escrito de trás para a frente. Semelhantemente, <0231> e <2013> estão relacionados por inversão-retrógrada - cada um é a versão invertida e de trás para a frente do outro (Exemplo 321-d). Não se falou em retrógrado e inversão-retrógrada previamente porque se estava tratando principalmente com coleções não ordenadas (conjuntos). Agora que se está falando sobre segmentos ordenados, importa se algo é apresentado para a frente ou de trás para a frente.
Como os conjuntos de classes de notas, SEGCs podem ser reunidos em classe-SEGCs. SEGCs relacionados por inversão, retrogradação ou retroinversão pertencem à mesma classe-SEGC. Os quatro SEGCs do Exemplo 3-22 incluíndo <3102> são os quatro membros de uma única classe de SEGCs. Dos quatro membros dessa classe-SEGC, seleciona-se o que começa com a nota mais grave para agir como forma prima (analogamente à forma prima de uma classe de conjuntos). Os quatro fragmentos melódicos pertencem todos à classe-SEGC com forma prima <0231>.
As classe-SEGCs para os SEGCs de três e quatro notas estão listados no Quadro 3e (as classe-SEGCs proliferam rapidamente após aquelas). Abordar o contorno dessa maneira permite discutir perfís e gestos musicais com clareza, mas sem deixar de confiar em discriminações mais difíceis de notas , classes de notas e seus intervalos. Contornos podem ser particularmente reveladores, entretanto, quando estudados com relação a notas e classes de notas. Assim, torna-se possível discutir semelhanças de perfil na apresentação de diferentes classes de notas e, de modo contrário, perfis divergentes dados a membros da mesma classe de conjuntos.
Quadro 3-6: Classe-SEGC para SEGCs de três e quatro notas.
| Nome | Forma prima |
|---|---|
| 3-1 | <012> |
| 3-2 | <021> |
| 4-1 | <0123> |
| 4-2 | <0132> |
| 4-3 | <0213> |
| 4-4 | <0231> |
| 4-5 | <0312> |
| 4-6 | <0321> |
| 4-7 | <1032> |
| 4-8 | <0302> |
3.10.3 Contornos de dinâmicas e durações.
Contornos podem ser também úteis ao falar sobre elementos musicais além das notas. [...] Contornos podem ser particularmente valiosos ao falar sobre música indefinida quanto às notas, como muita música experimental escrita desde 1950. [No original há vários exemplos para ilustrar essas possibilidades, mas não serão incluídos nem comentados aqui. Em resumo, pode-se aplicar SEGCs a virtualmente qualquer elemento musical.]
Contornos podem ser representados por segmentos de contorno (SEGCs) os quais podem pertencer a classe-SEGCs.
