Introdução à teoria pós-tonal (4a. ed.).
4. Motivos, encadeamentos, harmonia.
4.1 Projeção compositiva.
Para organizar extensões musicais maiores e juntar notas que podem estar separadas no tempo, os compositores de música pós-tonal as vezes aumentam os motivos da superfície musical e os projetam sobre distâncias musicais significativas. Esse procedimento musical é as vezes chamado de projeção compositiva [no original: "composing-out"] ‒ é como dizer que um motivo da superfície musical é projetado compositivamente num nível mais profundo da estrutura (outros termos relacionados são "ampliação" [enlargement], "repetição oculta" [concealed repetition], "aninhamento" [nestling] e, "autossimilaridade" [self-similarity]. [O Exemplo 4-1 ao lado foi adaptado a partir do exemplo 4-4 de Straus extraído de Les Noces de Stravinsky.]
O Exemplo 4-1a mostra a melodia do início do ballet que consiste de [Si, Ré, Mi] (a apojatura com o Fá está excluída). No início da terceira cena o conjunto é transposto dois semitons mais agudos [Dó, Mi, Fá] e conclui com uma coda prolongada com repetições obsessivas de outra transposição agora três semitons mais aguda que o original: [Sol, Si, Dó]. A progressão de grande escala perpassa o ballet inteiro, projetando o modelo do motivo original (Exemplo 4-1b).

Conjuntos podem ser apresentados (projetados compositivamente) por sobre longos lapsos de tempo.
4.2 Ciclos de intervalos.
Quando se fala de projeção compositiva, fala-se sobre configurações motívicas que são específicas de uma determinada peça. Mas o movimento linear sobre extensões curtas ou longas também podem ser guiadas por configurações mais genéricas conhecidas como ciclos de intervalos. São padrões que resultam quando se começa com uma determinada classe de notas e se move repetidamente por um único intervalo. Há seis desses ciclos de intervalos (Figura 4-1).
Movendo-se por i1 ou i11 obtêm-se o ciclo de semitons, ou ciclo-1, ou C1. Mover-se em torno do ciclo no sentido horário envolve o movimento por i1; mover-se no sentido anti-horário envolve o movimento por i11. Seja como for, o ciclo perpassa pelas doze classes de notas antes de retornar ao seu ponto de partida. Como resultado, só há um ciclo-1. Entretanto, há dois ciclos-2, um movendo-se pelas classes de notas pares e um pelas classes de notas ímpares. Os números subscritos no centro dos círculos identificam o conteúdo das classes de notas do ciclo: C20 contém a classe de notas 0 e C21 contém a classe de notas 1. Há três ciclos-3, correspondentes aos três acordes de sétima diminuta: C30 contém a classe de notas 0, C31 a classe de notas 1 e, C32 contém a classe de notas 2. E há quatro ciclos-4, correspondentes às quatro tríades aumentadas, novamente distinguidas por seu conteúdo de classes de notas. O ciclo-5 é o familiar "círculo de quartas ou quintas". Como o C1, há somente um ciclo-5, porque C5 perpassa pelas doze [classes de] notas antes de retornar ao ponto de partida. Há seis cilcos-6, cada qual correspondendo a um dos seis trítonos.
4.2.1 Movimentos cíclicos lineares.
Ciclos de intervalos as vezes moldam e direcionam movimentos lineares na música pós-tonal. O Exemplo 4.2 dá uma amostra de interação entre o ciclo-2 e o ciclo-5. [Leia-se o texto do item 4.2.2.]
4.2.2 Harmonias cíclicas.
Um conjunto cíclico é aquele que consiste de um ciclo de intervalos inteiro ou um segmento de um ciclo. Conjuntos cíclicos desempenham um papel proeminente na música pós-tonal, moldando tanto a harmonia quanto a melodia. No Exemplo 4-3 a melodia consiste de segmentos de dois ciclos-2 e a harmonia de segmentos de C5. Observe-se que há uma afinidade entre C2 e C5: a cada duas notas do ciclo-5 obtém-se um ciclo-2.
As importantes grandes coleções que são o tópico principal do próximo capítulo têm suas origens nos ciclos de intervalos. A escala cromática corresponde a C1. As duas coleções de tons inteiros correspondem aos dois ciclos-2. A coleção octatônica resulta de uma combinação de quaisquer dois dos três ciclos-3. A coleção hexatônica resulta da combinação de qualquer dos ciclos-4 pares (C40 ou C42) com qualquer dos ciclos-4 ímpares (C41 ou C43). (Combinando dois ciclos-4 pares ou dois ímpares produz a coleção de tons inteiros.) A coleção diatônica corresponde a quaisquer segmentos contíguos de sete notas de C5 (e a coleção pentatônica corresponde a qualquer segmento de cinco notas de C5). Os ciclos-6 podem ser combinados de várias maneiras para produzir coleções de tons inteiros ou coleções octatônicas.
4.2.3 Máxima uniformidade.
Os ciclos de intervalos também dão surgimento a harmonias que são maximamente uniformes, isto é, tão amplamente dispersas quanto possível em torno do mostrador de relógio de classes de notas. Se se tem duas notas e a tarefa é posicioná-las no mostrador de relógio de classes de notas de modo que elas fiquem o mais amplamente espaçadas possível, colocasse-as afastadas por um trítono. A harmonia C6, (cc(06), é assim a díade maximamente uniforme. Similarmente, a harmonia C4, cc(048), é o tricorde minimamente uniforme; a harmonia C3, cc(0369), é o tetracorde maximamente uniforme; e a harmonia C2, cc(02468A), é o hexacorde maximamente uniforme. E os pentacordes? Não se pode distribuir cinco classes de notas perfeitamente uniformes em torno do mostrador de relógio de classes de notas. O jeito maximamente uniforme de arranjá-las corresponde à coleção pentatônica cc(02479). Que corresponde a qualquer segmento de cinco notas de C5.
O que é verdade para essas classes de conjuntos maximamente uniformes é também verdade para seus complementos: a coleção diatônica (complemento da coleção pentatônica e correspondente a qualquer segmento de sete notas do ciclo-5) é o septacorde maximamente uniforme; a coleção octatônica (complemento de (0369) e correspondente a quaisquer dois ciclos-3) é o octacorde maximamente uniforme; a coleção eneatônica (complemento de (048) e correspondente a quaisquer três cilcos-4) é o nonacorde maximamente uniforme; e a classe de conjuntos com nome de Forte 10-6 é o decacorde maximamente uniforme. Harmonias maximamente uniformes, assim como os ciclos de intervalos dos quais elas se originam, frequentemente despertam o interesse de compositores e teóricos.
Harmonias que são quase uniformes (i.e., conjuntos maximamente uniformes onde uma nota foi ajustada por um semitom) também desempenharam um papel musical significativo historicamente. Uma (06) minimamente alterada é uma quarta ou uma quinta justas (a mais consonante das díades); uma (048) minimamente alterada é uma tríade maior ou menor; uma (0369) é (0258), tradicionalmente um acorde de sétima da dominante ou sétima meio-diminuta; uma (02468A) minimamente alterada é uma forma do "acorde místico" de Scriabin; as escalas menor harmônica e menor melódica ascendente são formas minimamente alteradas da coleção diatônica maximamente uniforme (Quadro 4-1).
Quadro 4.1: classes de conjuntos maximamente uniformes.
| Cardinalidade | Cc maximamente uniforme | No relógio | Origem cíclica | Quase uniforme |
|---|---|---|---|---|
| 2 | 2-6 (06) Trítono | 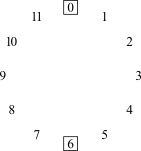 | C6 | 2-5 (05) Quarta/quinta justas |
| 3 | 3-12 (048) Tríade aumentada | 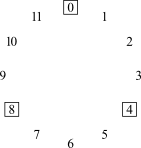 | C4 | 3-11 (037) Tríade consonante maior ou menor |
| 4 | 4-28 (0369) Acorde de sétima diminuta | 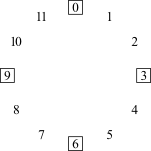 | C3 | 4-27 (0258) Acorde de sétima da dominante ou de sétima meio-diminuta |
| 5 | 5-35 (02479) Coleção pentatônica | 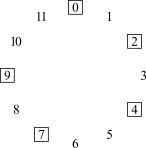 | Segmento de cinco notas de C5 | |
| 6 | 6-35 (02468A) Coleção tons-inteiros | 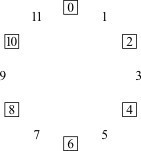 | C2 | 7-34 (013468A) Escala menor melódica ascendente. Escala acústica 7-32 (0134689) Escala menor harmônica |
| 7 | 7-35 (013568A) Coleção diatônica | 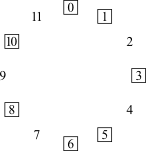 | Segmento de sete notas de C5 | 2-5 (05) Quarta/quinta justas |
| 8 | 8-28 (0134679A) Coleção octatônica | 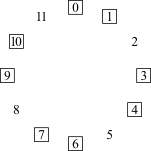 | Quaisquer dois C3 | |
| 9 | 9-12 (01245689A) Coleção eneatônica (nonatônica) | 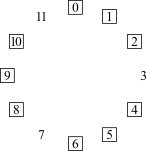 | Quaisquer três C4 | |
| 10 | 10-6 (012346789A) |  | Quaisquer cinco C6 |
4.2.4 Ciclos de combinação.
Ciclos de intervalos envolvem o movimento repetido por um único intervalo. Ciclos de combinação envolvem a alternância de dois intervalos diferentes. A Figura 4-2 ilustra os ciclos de combinação relacionados: <1,8>, <1,3> e <3,8>. Estes são intervalos ordenados de classes de notas e os caracteres angulados (sinais de maior que e menor que) indicam que os próprios intervalos ocorrem em uma ordem específica, a saber, em alternância.
Na Figura 4-2a, pode-se começar em qualquer classe de notas e percorrer o círculo alternando intervalos 1 e 8. Há três ciclos de combinação <1,8> de classes de notas distintas, correspondentes às três escalas octatônicas. A cada duas notas encontra-se o ciclo-3 (acordes de sétima diminuta). Cada ciclo de combinação pode ser entendido como dois ciclos simples entrelaçados. O intervalo do ciclo simples será a soma dos dois intervalos do ciclo de combinação. Aqui, o ciclo de combinação <1,8> envolve dois ciclos-9 entrelaçados (= a ciclos-3 na direção oposta), pois 1 + 8 = 9. Na Figura 4-2 os ciclos simples subjacentes estão escritos no centro dos círculos, enquanto ao ciclo de combinação está escrito em torno da circunferência do círculo.
Na Figura 4-2b há a alternância dos intervalos 1 e 3. Os quatro ciclos de combinações são gerados por diferentes combinações de ciclos-4 (tríades aumentadas). Os quatro ciclos de combinação <1,3> correspondem às quatro escalas hexatônicas.
Na Figura 4-2c a alternância dos intervalos 3 e 8 produzem uma sequência de classes de notas que requer vinte e quatro movimentos antes de voltar ao seu ponto de partida (com cada uma das doze classes de notas ocorrendo duas vezes). Este ciclo de combinação pode ser pensado como dois ciclos-1 entrelaçados. O que todos os ciclos de combinação da Figura 4-2 têm em comum é que qualquer segmento de três notas é um membro da cc(014). Pode-se pensar nos ciclos de combinação como meios de se mover sistematicamente pelos membros de uma classe de conjuntos particular.
Os segmentos de ciclos de combinação, assim como os ciclos de intervalos simples que os constituem, frequentemente guiam linhas melódicas pós-tonais. Na melodia do Exemplo 4-4, virtualmente todos os agrupamentos de três notas são membros da cc(014). Eles são usualmente apresentados como alternância de dois intervalos, sejam 1 e 8 ou seus complementos, 11 e 4. Como resultado, é possível traçar os movimentos melódicos nos três ciclos <1,8> mostrados na Figura 4-2a, movendo-se tanto no sentido horário quanto anti-horário em torno do círculo.
Na Figura 4-3 [o ciclo de combinação <1,6>] alterna 6 e -1. O ciclo de combinação inteiro faz 24 movimentos para retornar ao seu ponto de partida (cada classe de notas aparece duas vezes no ciclo) [...]. Todos os tricordes melódicos são membros da cc(016) numa espécie de cadeia sem fim [Exemplo 4-5].
A transposição sistemática de uma classe de notas por um único intervalo produz um ciclo de intervalos; a transposição sistemática de uma classe de notas por um par de intervalos alternados produz um ciclo de combinação.
4.3 Encadeamentos. [*]
A discussão sobre projeção compositiva e ciclos de intervalos preocupou-se com os meios pelos quais uma nota pode ser ouvida movendo-se para outra e, especialmente, com as linhas melódicas resultantes. Agora aborda-se um aspecto algo mais abstrato da organização linear, especificamente, o movimento de vozes transformativas. Uma linha é algo literal e concreto; uma voz resulta da transformação harmônica subjacente. Uma maneira útil de descrever o encadeamento na música pós-tonal envolve seguir o contraponto de classes de notas criado por transposição e inversão. Como já foi visto, a transposição e a inversão envolvem o mapeamento de notas de um conjunto para outro. Aqueles mapeamentos podem ser entendidos como compreendendo vozes transformativas pós-tonais.
4.3.1 Transposição e inversão.
No Exemplo 4-6 os acordes são todos membros da classe de conjuntos (016). As linhas horizontais e diagonais traçam o mapeamento das classes de notas induzidas pelas operações especificadas. Três vozes transformativas movem-se através da progressão. Uma começa em Mi e desce para a base do terceiro acorde antes de retornar à sua posição original no registro mais agudo. A voz intermediária e a voz mais grave também se movem pelos acordes e retornam à sua posição original no final. O segundo nível de análise simplifica a progressão de cinco acordes em dois movimentos inversivos, cada um deles troca as partes vocais com a parte que soa mais grave. Finalmente, o terceiro nível descreve a progressão como a transposição à T8 (na verdade uma transposição de notas quatro semitons abaixo) do primeiro acorde para o último acorde. Em cada nível, as harmonias estão unidas pelo movimento das vozes.
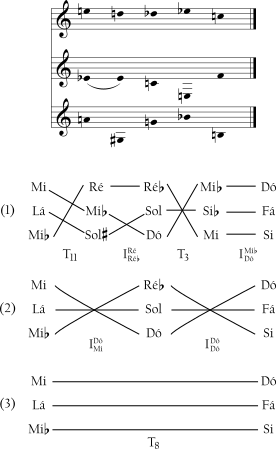
4.3.2 Transposição difusa e inversão (com deslocamento) [*].
[...] No Exemplo 4-7 os seis acordes representam três diferentes classes de conjuntos: o primeiro e o segundo acordes estão relacionados por transposição, assim como estão os terceiro, quarto e quinto acordes. O problema analítico é conectar o segundo acorde ao terceiro e o quinto ao sexto. Numa situação como essa, pode ser útil imaginar que os acordes estão quase, mas não totalmente relacionados por transposição (ou inversão). Na progressão do segundo para o terceiro acorde pode-se descrever a relação como quase-T2 ou um T2-difuso: três das vozes desviam de T2, mas o fazem por tão pouco quanto possível, por apenas um semitom cada (Exemplo 16a). Movendo-se do quinto para o sexto acorde, o desvio de uma transposição real é ainda menor - somente uma voz está fora, e está fora por somente um semitom. Transposições (ou inversões) que estão um pouco fora são designadas com um asterisco, e a quantidade de desvio, conhecido como deslocamento está indicada entre parênteses. No encadeamento, os mapeamentos reais estão mostrados com linhas sólidas e os mapeamentos difusos com uma linha pontilhada.

Na passagem os movimentos transpositivos individuais combinam-se para criar um único grande movimento transpositivo: do primeiro acorde para o último numa transposição difusa à *T5, com um pequeno desvio de somente dois semitons (Exemplo 4-7b). A progressão como um todo, abarcando membros de três diferentes classes de conjuntos, pode assim ser ouvida como um único gesto unificado, com um claro encadeamento paralelo.
Certamente os encadeamentos não precisam ser paralelos. Na passagem mostrada no Exemplo 4-8, há cinco acordes representando quatro classes de conjuntos diferentes. As transposições e inversões difusas que conectam os acordes produzem encadeamentos transformativos nos quais as vozes se cruzam.

Os mapeamentos induzidos por T e I podem ser entendidos como vozes transformativas. Na sucessão de harmonias relacionadas por T e I esses mapeamentos compreendem encadeamentos transformativos.
4.4 Espaço de classes de notas.
Na discussão sobre o encadeamento falou-se sobre conjuntos de classes de notas reais e os meios pelos quais notas individuais de um conjunto se movem para notas individuais em outro conjunto. Também é possível falar mais abstratamente sobre o encadeamento entre classes de conjuntos. Imagine mover-se de uma classe de conjuntos para outra em um espaço de classes de conjuntos multidimensional.
4.4.1 Espaço de encadeamentos para tricordes.
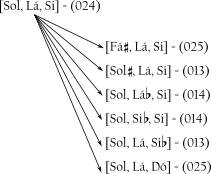
Dado um conjunto pertencente a uma classe de conjuntos, pode-se perguntar quanto ajuste em semitons seria necessário para torná-lo um membro de uma classe de conjuntos diferente. Como exemplo, o tricorde [Sol, Lá, Si], um membro da cc(024). Ajustando cada uma das suas notas de cada vez tanto um semitom acima quanto um abaixo, produz seis tricordes diferentes representando três classes de conjuntos (Figura 4-4). Em termos gerais, pode-se dizer que a cc(024) está deslocada pela distância de somente um semitom de encadeamento das cc(013), cc(014) e cc(025).
Ao aplicar o mesmo procedimento a todas as classes de tricordes, obtém-se um mapa como o da Figura 4-5.
Neste espaço de encadeamentos as classes de tricordes estão mostradas com relativa proximidade umas com as outras. Quanto mais próximos dois tricordes estiverem no mapa, menos distância em semitons há entre eles. Cada linha do mapa representa um semitom de deslocamento (isto é, um semitom de ajuste de encadeamento ou distância de encadeamento), e as distâncias acumulam-se de modo consistente. De (012), um semitom de deslocamento leva para (013), dois semitons de deslocamento levam para (014) ou (024), três semitons de deslocamento levam para (015) ou (025) e assim por diante até o máximo de seis semitons de deslocamento entre (012) e (048).
A quantidade de movimentos de tricorde para tricorde no mapa corresponde às quantidades de deslocamento na discussão prévia sobre encadeamento transformativo. Revendo-se o Exemplo 4-8 vê-se que há uma progressão de cinco tricordes: (014) - (016) - (025) - (015) - (014). Ao se traçar aquela progressão no mapa da Figura 4-5, fica-se ciente de um salto para longe de (014) e uma circulação gradual de volta para ela. O mapa tricordal sugere a possibilidade de entender uma passagem de música como uma jornada através do espaço de encadeamentos definido pelo deslocamento de semitons - as vezes os movimentos serão para destinos próximos, envolvendo apenas uma pequena quantidade de ajustamentos; outras vezes a música pode fazer amplos saltos harmônicos.
4.4.2 Espaço de encadeamentos para tetracordes.
Conforme a quantidade de conjuntos aumenta, torna-se mais difícil representar o espaço numa página bidimensional. [*].
Assim como o mapa para tricordes, este mapa permite visualizar e interpretar progressões como as mostradas no Exemplo 4-9 [**].
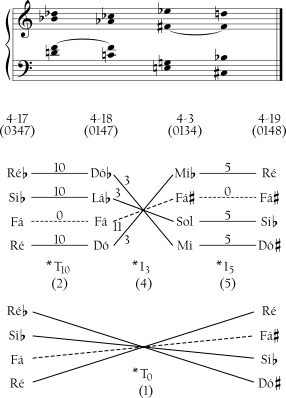
As quantidades de deslocamento em cada encadeamento transformativo correspondem exatamente às distâncias no espeço de encadeamentos. Do primeiro acorde para o segundo a progressão se move por *T10 com um deslocamento de 2, e no mapa, (0347) está dois cliques afastado de (0147). As próximas duas progressões envolvem graus maiores de deslocamento correspondentes a grandes saltos no espaço. Do primeiro acorde para o último, entretanto, há um deslocamento de somente 1, e (0347) e (0148) repousam um ao lado do outro no espaço. A progressão salta à volta, mas retorna próxima de onde começou.
4.4.3 Qualidade harmônica.
Os mapas para tricordes e tetracordes estão dispostos de modo surpreendentemente semelhante. Em ambos os mapas, as classes de conjuntos cromáticas, mais compactas e comprimidas estão em uma extremidade do espaço e as mais dispersas e abertas estão espaçadas uniformemente na outra extremidade. Para os tricordes, os extremos são (012), o tricorde cromático, e (048), a tríade aumentada, que é o tricorde maximamente uniforme (i.e. o meio mais igual de arranjar as três notas em torno do mostrador de relógio de 12-cn). Para os tetracordes, os extremos são (0123), o tetracorde cromático, e (0369), o acorde de sétima diminuta, que é o tetracorde maximamente uniforme. Em geral, as harmonias que são tradicionalmente consideradas mais tensas e dissonantes são encontradas na direção de um dos extremos dos espaços, enquanto as harmonias consideradas mais relaxadas e consonantes são encontradas na direção do outro extremo.
Esses espaços de encadeamento assim permitem mensurar não somente a distância entre quaisquer duas harmonias, mas também a direção da progressão, se é dirigida para um estado de relativa cromaticidade (tensão) ou uniformidade (relaxamento). Ao olhar-se novamente o Exemplo 4-8 pode-se imaginar a progressão começando e terminando num estado de relativa compressão e cromaticidade, com uma sessão interna que está relativamente aberta e relaxada. A progressão do Exemplo 4-9 funciona exatamente ao contrário: o primeiro e o último acordes são relativamente consonantes comparados com o denso e cromático terceiro acorde. Esses espaços de encadeamento permitem interpretar tanto a distância quanto a direção de uma progressão de harmonias.
As classes de conjuntos podem ser arranjadas num espaço de encadeamentos onde classes de conjuntos adjacentes requerem ajustamentos de apenas um semitom. Em tais espaços, as classes de conjuntos cromaticamente mais densas situam-se em uma extremidade enquanto as classes de conjuntos mais uniformemente distribuídas situam-se na outra.
4.5 Inversão contextual.
O movimento de harmonia para harmonia na música pós-tonal é frequentemente motivado por T ou I (tanto puras quanto difusas) e podem ser traçadas nos espaços de encadeamento recém discutidos. Às vezes, entretanto, o movimento harmônico segue um caminho mais idiossincrático, determinado pela estrutura das próprias harmonias. Uma força motivadora pode ser a inversão contextual com nota comum preservada: uma harmonia inverte-se em torno de uma ou mais de suas notas para tornar-se outra harmonia. A inversão genérica geral (In) é definida com referência a classes de notas específicas, por exemplo, I5 é a inversão que mapeia Dó (0) em Fá (5), Dó (1) em Mi (4) e assim por diante, e aqueles mapeamentos acontecerão independentemente da natureza da harmonia que está sendo invertida. A inversão contextual, entretanto, é definida com referência a uma característica particular da harmonia que está sendo invertida. "Inverta uma tríade menor em torno da sua terça maior" e "inverta uma série em torno da sua primeira nota" são exemplos de inversão contextual: o efeito da inversão sobre as classes de notas irão variar dependendo do contexto musical. Inversões contextuais são particularmente interessantes quando elas ocorrem em cadeias, dando origem a progressões estendidas de harmonias (sejam elas expressas como acordes ou segmentos melódicos, ou alguma combinação dos dois).
4.5.1 Cadeia e espaço para (014).
Com referência à melodia do Exemplo 4-4 [*], discutida em termos de ciclos de combinação, pode-se pensar nas instâncias de (014) que pervadem a melodia como elos numa cadeia de inversões contextuais (o Exemplo 4-10a reproduz os últimos seis compassos da melodia).
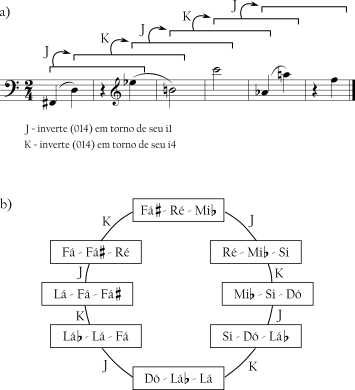
Define-se duas inversões contextuais:
- J gira (014) em torno de seu i1. As duas notas que formam i1 mapeiam-se uma na outra.
- K gira (014) em torno de seu i4. As duas notas que formam i4 mapeiam-se uma na outra.
Nesse sentido, a melodia pode ser pensada como uma cadeia interligada de J e K, com seis formas de (014) como elos da corrente. Um ciclo completo de inversões JK está mostrado no Exemplo 4-10b.
Uma progressão como essa é as vezes referida como uma cadeia-RI pois cada motivo está relacionado por retroinversão [retrógrado da inversão] com os motivos antes e depois dele. Assim como com os espaços de encadeamentos, este espaço de inversão contextual é um local útil para traçar a melodia de Webern. Ela começa no topo do círculo e o vai percorrendo até quase voltar ao seu ponto de partida.
4.5.2 Cadeia e espaço para Si, Sol, Lá, Si.
[Há uma análise de Stravinsky, "Musick to heare", das Três canções de Shakespeare com 3 inversões contextuais definidas e um espaço referente à série. Não foi incluído aqui por razões diversas].
A inversão contextual envolve a inversão de um conjunto com respeito a uma de suas características internas. Inversões contextuais podem ocorrer únicas ou em cadeias.
4.6 Pós-tonalidade triádica.
As tríades maiores e menores são harmonias básicas em muitos estilos pós-tonais diferentes de composição, incluindo neoclassicismo, neotonalismo e minimalismo. Em muitos casos, encontram-se progressões estendidas de tríades que não estão restritas pelas normas da tonalidade tradicional. Em particular, as tríades não se relacionam umas com as outras funcionalmente, como pré-dominantes, dominantes ou tônicas. Tal música é triádica, mas ainda assim distintamente pós-tonal.
4.6.1 Transformação triádica.
Uma classe particular de transformações triádicas envolve inversão contextual com nota comum preservada e encadeamento parcimonioso. A inversão contextual em tríades significa que para ir de uma tríade para a próxima, inverte-se em torno de uma ou duas das notas da primeira tríade: isso sempre conduz de uma tríade maior para uma menor e vice-versa, porque tríades maiores e menores estão relacionadas por inversão de classes de notas. O encadeamento parcimonioso significa que as tríades estão conectadas pelo meio mais suave possível, com as vozes movendo-se o mínimo possível. O encadeamento mais parcimonioso envolve duas vozes sem movimento (há duas notas em comum) e a voz que faz o movimento o faz por somente um semitom. Um encadeamento ligeiramente menos parcimonioso envolve duas vozes sem movimento e uma movendo-se por dois semitons, ou uma voz sem movimento e duas vozes movendo-se por um semitom cada.
O Quadro 4-2 [*] ilustra seis transformações triádicas: as três primeiras retêm duas notas em comum; as três últimas retêm uma nota em comum. (As fundamentais das tríades estão dadas com letras maiúsculas com um sinal de + ou - para indicar a qualidade da tríade.)
Quadro 4.2: seis transformações triádicas.
| Nome | Descrição | Inversão contextual | Encadeamento parcimonioso | Exemplo |
|---|---|---|---|---|
| H (Homônima) | A tríade maior e a menor compartilham a mesma fundamental. | Inverte em torno da quinta justa compartilhada. | Um voz se move por semitom. | 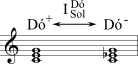 |
| S (Sensível) | A terça de uma tríade maior torna-se a fundamental de uma menor (e vice-versa). | Inverte em torno da terça menor compartilhada. | Um voz se move por semitom. | 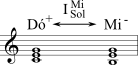 |
| R (Relativa) | A fundamental de uma tríade maior torna-se a terça de uma menor (e vice-versa). | Inverte em torno da terça maior compartilhada. | Um voz se move por dois semitons. |  |
| H' (Deslizar) | Tríades maiores e menores compartilham a mesma terça. | Inverte em torno da nota que não é parte da quinta justa. | Duas vozes se movem por semitom na mesma direção. | 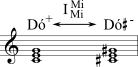 |
| S' | A fundamental de uma tríade maior torna-se a quinta de uma tríade menor (e vice-versa). | Inverte em torno da nota que não é parte da terça menor. | Duas vozes se movem por semitom na mesma direção. |  |
| R' | A quinta de uma tríade maior torna-se a fundamental de uma tríade menor (e vice-versa). | Inverte em torno da nota que não é parte da terça maior. | Duas vozes se movem por dois semitons na mesma direção. | 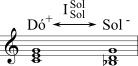 |
A primeira é chamada H, e ela relaciona uma tríade maior e uma menor que contêm a mesma quinta justa e compartilha a mesma fundamental, como Dó+ e Dó–. Quando Dó maior se move para Dó menor (ou vice-versa), o Mi se move para o Mi (ou vice-versa) - uma única voz se move por semitom. Estas duas tríades estão relacionadas pela inversão que mapeia Dó em Sol um no outro. A segunda transformação é chamada S e ela relaciona uma tríade maior e uma menor que contém a mesma terça menor - a terça da tríade maior torna-se a fundamental da tríade menor (e vice-versa). Ao mover Dó+ para Mi–, por exemplo, inverte-se em torno da sua terça menor compartilhada, o que produz encadeamento parcimonioso, com o Dó movendo-se um semitom para Si. A terceira transformação é chamada R, e ela relaciona uma tríade maior e uma menor que contém a mesma terça maior. Inverter em torno da terça maior compartilhada faz uma voz mover-se por dois semitons. Mover-se de Dó+ para Lá–, por exemplo, envolve a inversão que troca Dó com Mi e move o Sol para o Lá. Essas três transformações são amplamente usadas no música pós-tonal (e na música cromática do final do Século XIX também).
A essas, adicionam-se mais três: H', S' e R'. H, S e R retêm uma díade e viram uma única nota em torno dela; H', S' e R' fazem exatamente o oposto e são assim os seus anversos: elas retêm uma única nota e viram a díade. Destas, H' (também chamada DESLIZADA) tem particularmente grande circulação na música pós-tonal. Ela relaciona uma tríade maior e uma menor que compartilham a mesma terça, como Dó+ e Dó–. Essa transformação envolve inversão contextual em trno de uma única nota (em vez de um par de notas) e ela faz duas vozes se moverem, embora elas se movam somente por semitom.
As transformações podem ocorrer independentemente, ou (como nas inversões contextuais discutidas anteriormente) elas podem ser combinadas em cadeia e progressões maiores. Por exemplo, considere-se a cadeia-SH (uma alternância de S e H). Ao se começar com Dó+ e movendo-se pela alternância de H e S, cria-se um ciclo de seis tríades : tríades maiores e menores construídas sobre Dó, Mi e Lá. Cada movimento em torno do círculo envolve a mudança de uma única nota por um semitom, e assim o encadeamento conforme se move pelo círculo é tão parcimonioso quanto possível. O ciclo como um todo envolve apenas seis classes de notas diferentes, que correspondem a uma das quatro coleções hexatônicas, (014589) (a ser discutida mais completamente no próximo capítulo). As tríades que estão opostas umas às outras no círculo (como Dó+ e Sol– são conhecidas como polos hexatônicos - elas não têm notas em comum e juntas exaurem a coleção hexatônica. Os quatro sistemas hexatônicos ou ciclos-SH estão ilustrados na Figura 4-6.
Um ciclo diferente, ciclo-HSR está ilustrado na Figura 4-7. Este ciclo consiste de seis tríades (três maiores e três menores) e todas elas compartilham uma única classe de notas, neste caso a classe de notas Dó. Cada tríade no ciclo difere de suas vizinhas por somente um ou dois semitons. As tríades colocadas opostas umas às outras estão relacionadas por H' (DESLIZADA), S' ou R'.
4.6.2 Outras progressões de tríades.
Em algumas progressões de tríades, o caminho pode ser definido por ciclos de intervalos, por simetria inversiva ou pela projeção compositiva de um motivo. No Exemplo 4-12 [*], o início de Makrokosmos de Crumb, todas as doze tríades menores estão arrumadas para seguir o ciclo-1. As fundamentais das tríades da parte da mão direita descendem descem por semitom através de uma oitava inteira. Ao mesmo tempo, as notas reais gradualmente ascendem das profundezas, com cada nota movendo-se em direção ascendente para a posição mais próxima disponível no acorde seguinte. Cada tríade da mão direita está precedida por uma tríade escrita como apojatura ao intervalo de um trítono mais grave na mão esquerda.

Um tipo diferente de padronização está evidente no Exemplo 4-13 [**], o final de uma canção orquestral de Britten. Ali, as tríades são todas maiores, e estão dispostas simetricamente em torno de Ré maior. Dó+ e Mi+ circundam Ré+ simetricamente. O Dó+ na cadência equilibra o Mi+ no início da passagem. A armadura e o acorde final ambos sugerem que Ré+ é a tônica, mas sua tonicidade é criada por simetria inversiva, não por funções harmônicas tradicionais.

Um terceiro tipo de caminho triádico está ilustrado no Exemplo 4-14 [***], de uma quarteto de cordas de Shostakovich. No final da passagem, ouve-se uma progressão de quatro tríades menores: Sol-, Lá-, Si- e Ré– (com a terça faltando). As tríades são precedidas por uma melodia de doze notas no violoncelo (somente o final da melodia está mostrado ali). As notas finais da melodia (Ré, Mi e Fá) retornam como notas mais agudas das tríades. Nesse sentido, as tríades simplesmente harmonizam de um modo paralelo e não funcional a melodia prévia. Há um vínculo motívico mais sutil adicional entre a melodia e as tríades. Um membro da cc(0137) está embutido na melodia, e a sucessão das fundamentais das tríades descrevem outro membro da mesma classe de conjuntos. Assim, tanto a melodia do soprano quanto as fundamentais da progressão seguem um caminho motívico.

