Introdução à teoria pós-tonal (4a. ed.).
2. Conjuntos de classes de notas.
2.1 Conjuntos de classes de notas.
Os conjuntos de classes de notas são os blocos constitutivos de muita música pós-tonal. Um conjunto de classes de notas é uma coleção não ordenada de classes de notas. Pode-se pensar neles como um motivo do qual muitas das características identificadoras: registro, ritmo, ordem, foram removidas. O que resta é simplesmente as classes de notas básicas e a identidade classe-intervalar de uma ideia musical. (Ver o Exemplo 2-1a e 2-1b ao lado.)
Um conjunto de classes de notas é uma coleção não ordenada de classes de notas.
2.2 Forma normal.
2.2.1 Colocando um conjunto em forma normal.
Para reconhecer um conjunto de classes de notas não importando como ele esteja presente na música, é útil colocá-lo em uma forma simples, compacta, facilmente reconhecível chamada forma normal. (É representada por colchetes com os números separados por vírgulas, e.g.: [0, 1, 3].) (Ver o Quadro 2-1.)
Quadro 2-1: colocando conjuntos em forma normal.
| Procedimento | Exemplo 1 | Exemplo 2 | Exemplo 3 |
|---|---|---|---|
Excluindo dobramentos, escreva as classes de notas como se fossem uma escala ascendendo dentro da oitava. (Haverá tantas maneiras diferentes de fazer isso quantas classes de notas houver no conjunto, já que a ordenação pode começar em qualquer uma delas.) Calcule o âmbito intervalar de cada uma. | Lá-Sib-Fá Lá→Fá = 8 | Fá-Láb-Lá-Dó# Fá→Dó# = 8 | Dó-Mi-Sol#-Lá-Si Dó→Si = 11 |
Regra 1: A ordenação que tem o menor intervalo da primeira para a última (da mais grave para a mais aguda) é a forma normal. | Fá-Lá-Sib Fá→Sib = 5 | Fá-Láb-Lá-Dó# Fá→Dó# = 8 | Mi-Sol#-Lá-Si-Dó Mi→Dó = 8 |
Regra 2: Se há um empate na Regra 1, a forma normal é a ordenação que compacta as classes de notas mais próximas de um extremo ou de outro. Haverá uma maior concentração relativa de grandes intervalos no topo ou na base. | Fá Láb Lá Dó# | Mi Sol# Lá Si Dó | |
Se há mais de uma forma normal (como haverá para conjuntos simétricos por inversão, a serem discutidos posteriormente), prefira a que for mais compactada na base. | [Sol#, Lá, Si, Dó, Mi] é mais compacta na base (intervalos maiores no topo), então esta é a preferida. |
2.2.2 Usando o mostrador de relógio de classes de notas.
Em vez de seguir passo a passo o procedimento, é possível determinar a forma normal simplesmente por inspecionar o conjunto disposto num mostrador de relógio de classes de notas. (Ver a Figura 2-1.)
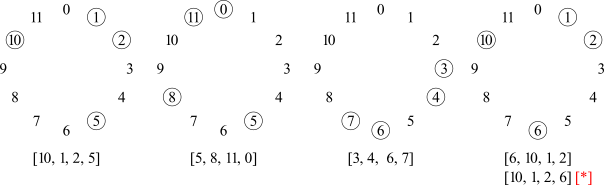
A forma normal é uma maneira simples e compacta de escrever um conjunto de classes de notas.
2.3 Transposição (Tn).
2.3.1 Linha (ou série) de notas.
Tradicionalmente o termo transposição refere-se à transposição de uma linha (ou série) de notas. Por exemplo, quando transpomos uma melodia de uma tonalidade para outra, transpomos cada nota em ordem, por algum intervalo de nota. Isso preserva os intervalos ordenados de notas da melodia (i.e., seu contorno ou conformação de ascensos e descensos). Ver o Exemplo 2-2a ao lado.
2.3.2 Linha (ou série) de classes de notas.
As coisas são diferentes quando transpomos uma linha (ou série) de classes de notas. Agora iremos transpor cada classe de notas de uma linha, em ordem, por algum intervalo de classes de notas.
O contorno das duas linhas pode resultar diferente, mas as duas linhas preservam duas características importantes. Primeiro, para cada classe de notas da primeira melodia, a classe de notas correspondente da segunda linha está separada pelo mesmo intervalo de classes de notas. Segundo, os intervalos ordenados de classes de notas entre notas adjacentes nas duas melodias são os mesmos (têm a mesma sucessão). Por isso, apesar de suas diferenças óbvias, elas ainda soam muito semelhantes. Ver o Exemplo 2-2b ao lado.
Representa-se a operação de transposição de classes de notas como Tn, onde T significa transposição e n é o intervalo de transposição (também conhecido como “número de transposição”).
2.3.3 Conjuntos de classes de notas.
Agora devemos considerar a possibilidade de transpor não uma linha, mas um conjunto de classes de notas. Um conjunto é uma coleção sem ordem ou contorno específicos. Como resultado, a transposição de um conjunto não preserva nem a ordem nem o contorno. As transposições de um conjunto em geral são dadas em forma normal para facilitar a identificação.
Conjuntos que são traspositivamente equivalentes, contém os mesmos intervalos não ordenados de classes de notas. Isso lhes dá uma sonoridade semelhante. A transposição de um conjunto de classes de notas pode envolver muitas mudanças, mas ela preserva o conteúdo classe-intervalar. Ver o Exemplo 2-3a ao lado.
2.3.4 Níveis de transposição.
Geralmente há uma boa razão pela qual um compositor escolhe alguma transposição específica. às vezes o intervalo de transposição duplica um intervalo que está dentro do conjunto sendo transposto. As setas indicam o mapeamento que provoca a transposição. Ver o Exemplo 2-3b ao lado.
2.3.5 Transpondo um conjunto de classes de notas.
Para transpor um conjunto de classes de notas, simplesmente adiciona-se um único intervalo de classes de notas a cada membro de um conjunto. Por exemplo, para transpor [5, 7, 8, 11] pelo intervalo de classes de notas 8, adiciona-se 8 a cada elemento do conjunto para criar um novo conjunto: [1, 3, 4, 7] (Exemplo 2-4). Nesse caso se diz que "[1, 3, 4, 7] é T8 de [5, 7, 8, 11]" ou que "T8 mapeia [5, 7, 8, 11] em [1, 3, 4, 7]". Aqui, aplicar T8 à 5 transforma-o em ou mapeia-o em 1, T8 mapeia 7 em 3 e assim por diante. Se o primeiro conjunto estiver em forma normal, sua transposição também estará em forma normal.

2.3.6 Reconhecendo conjuntos relacionados por transposição.
Se dois conjuntos estão relacionados por transposição ao intervalo n, para cada nota do primeiro conjunto haverá uma nota correspondente no segundo conjunto separada por n semitons. Descobrir essa correlação um a um é mais fácil quando os dois conjuntos estão em forma normal.
Conjuntos de classes de notas relacionados por transposição têm a mesma sucessão de intervalos lendo-se da esquerda para a direita (Exemplo 2-5).

Para descobrir o intervalo de transposição, compare os elementos correspondentes. Cada membro do segundo conjunto dista n semitons do membro correspondente do primeiro conjunto. Pode-se ver diretamente nas duas formas normais, mas pode-se descobrir usando a fórmula para calcular intervalos ordenados de classes de notas: para cada classe de notas x do primeiro conjunto para cada classe de notas do segundo conjunto, o intervalo é y - x. No caso do Exemplo 2-5 a seguir, y - x = 8 (Exemplo 2-6).

2.3.7 Nodos, setas e redes.
Pode-se representar relações de transposição usando uma combinação de nodos (indicados como círculos que contém algum elemento musical, tais como uma nota ou um conjunto) e setas (para mostrar a operação que conecta os nodos). A mesma operação que move a música de uma nota para outra nota também a move de um conjunto para outro conjunto. As Redes são agrupamentos de nodos (que podem ter conteúdos diferentes) e setas. Quando duas redes são iguais, tecnicamente diremos que as duas redes são isográficas (Figura 2-2).
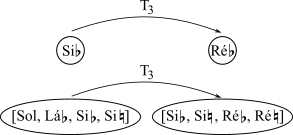
2.3.8 Inversa [reversa].
Ao transpor um Conjunto 1 à T3, ele se mapeia no Conjunto 2. O que acontece ao reverter-se a ordem dos dois conjuntos e se transpõe o Conjunto 2 de volta para o Conjunto 1? Se T3 nos leva do Conjunto 1 para o Conjunto 2, então T9 levará de volta do Conjunto 2 para o Conjunto 1 (Figura 2-3).
![transposição inversa [reversa]](tpt_2/transp_inv_a.png)
Os números 3 e 9 são complementos mod 12 (i.e., eles somam 12). T3 e T9 são assim [operações] inversas uma da outra. Isso significa que se o Conjunto X e o Conjunto Y estão relacionados por Tn, então o Conjunto Y e o Conjunto X estarão relacionados à T12-n. Isso também significa que, como operações inversas, Tn e T12-n se cancelam: se ao começar com o Conjunto X, executar-se Tn e então T12-n, termina-se com o Conjunto X novamente (Figura 2-4).
![Operação inversa (reversa]](tpt_2/transp_inv_b.png)
Quando X é transposto para Y (sejam X e Y séries ou conjuntos de notas ou de classes de notas), cada nota de X é transposta para uma nota correspondente em Y e, X e Y compartilham o mesmo intervalo.
2.4 Inversão (In).
2.4.1 Número de índice (soma).
Quando se transpõe uma nota x à Tn, adiciona-se o intervalo n a x para produzir uma nova nota, y. Se as duas notas são conhecidas e se quer calcular o intervalo de transposição (o número de transposição), subtrai-se a nota x da nota y.
Se Tn(x) = y, então y = n + x. Logo y - x = n.
Quando se inverte uma nota x à In, subtrai-se a nota x do número de índice n para produzir uma nova nota y. Se as duas notas são conhecidas e se quer calcular o índice de inversão (o número de índice), adiciona-se a nota x à nota y.
Se In(x) = y, então y = n - x. Logo x + y = n.
Na expressão In n é o número de índice e ele representa a soma de quaisquer duas notas relacionadas por inversão. (Em muitas fontes padrão, incluindo edições prévias deste livro, a inversão é descrita como uma operação composta, TnI, onde I significa "inverter em torno de Dó" e Tn significa "transpor da maneira usual". Mas a aritmética é a mesma em ambos os casos. Tanto para TnI quanto para In, n é um número de índice (a soma de duas notas relacionadas por inversão.)
Pode parecer estranho que a adição tenha um papel tão importante ao falar sobre In. A ideia de subtrair duas notas, de descobrir a diferença entre elas, tem um claro sentido musical. Mas o que poderia significar, diga-se, adicionar Mi à Fá? Porque a soma de Mi e Fá é precisamente o valor de n que mapeia Mi em Fá e Fá em Mi sob In? Para entender imagine Mi e Fá num mostrador de relógio (Figura 2-5).
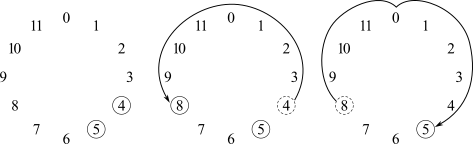
O Mi está em +4. Invertê-lo o envia para -4 (= 8, mod 12). Ou seja, Mi (+4) está invertido em Láb (-4 = 8 mod 12). Agora, para mapear o Mi invertido em Fá, deve-se transpô-lo a 4 (de volta para zero) mais 5 (que o leva para Fá). Ou seja, para ir de -4 para +5 move-se 4 + 5 = 9 semitons. Assim, In mapeia Mi em Fá. Pela mesma lógica, se se inverter o Fá, ele vai de +5 para -5. Agora para mapeá-lo em Mi , ele deve ser transposto para n = 9. Assim, I9 mapeia Fá em Mi e Mi em Fá. Na expressão In, n é a soma de x e y. Como visto, pode-se pensar nele como o intervalo entre -x (i.e., a inversão de x) e y.
2.4.2 Linha (ou série) de notas.
Como a transposição, a inversão é uma operação tradicionalmente aplicada a linhas (ou séries) de notas. Ao inverter uma linha de notas, a ordem é preservada e o contorno é revertido – cada intervalo ascendente é substituído por um descendente e vice-versa. Ver os Exemplos 2-7a e 2-7b ao lado.
2.4.3 Linha (ou série) de classes de notas.
Quando se inverte uma linha (ou série) de classes de notas, move-se num espaço modular de classes de notas. Ver o Exemplo 2-8 ao lado.
Note-se que In é a sua própria inversa: a operação que desfaz o efeito de uma operação. Ao inverter algo (uma nota, uma linha ou um conjunto) por alguma In e se quer voltar para onde começou, basta executar a mesma In novamente. Ao contrário, como discutido anteriormente, ao transpor algo à Tn, precisa-se executar a transposição complementar, T12-n, para voltar de onde começou.
Quando se inverte uma linha de classes de notas, cada intervalo de classes de notas na linha é substituído, em ordem, pelo seu complemento mod 12. Isso é, cada intervalo é revertido em direção: –1 (= 11) torna-se 1; –4 (= 8) torna-se 4; 1 torna-se –1 ( = 11); e assim por diante (Figura 2-6).
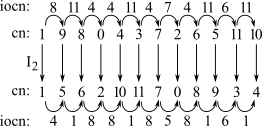
Ver também o Exemplo 2-9 ao lado.
2.4.4 Conjuntos de classes de notas.
Agora chega-se à inversão de um conjunto de classes de notas. Conjuntos escritos como imagens espelhadas um do outro quando em forma normal, estão relacionados por inversão. Assim como os conjuntos relacionados por transposição, os conjuntos relacionados por inversão têm o mesmo conteúdo classe-intervalar. Ver o Exemplo 2-10 ao lado.
Ao se comparar os dois primeiros conjuntos, observa-se que o primeiro tem os mesmos intervalos lidos de cima para baixo que o segundo tem lidos de baixo para cima. Conjuntos que podem ser escritos dessa maneira, como imagens espelhadas um do outro, estão relacionados por inversão. Ao comparar o primeiro conjunto com o terceiro vê-se que eles também estão escritos como imagens espelhadas um do outro e, portanto, estão relacionados por inversão. Assim como os conjuntos relacionados por transposição, os conjuntos relacionados por inversão têm o mesmo conteúdo classe-intervalar. Todos os três conjuntos do Exemplo 2-11 contém ci1, ci3 e ci4 somente e nenhum outro intervalo.

A Figura 2-7 resume as relações entre esses conjuntos e usa setas para indicar mapeamentos relevantes. A relação inversiva fica aparente quando os conjuntos estão escritos em forma normal: a primeira nota de um mapeia-se na última nota do outro, a segunda na antepenúltima e, assim por diante.
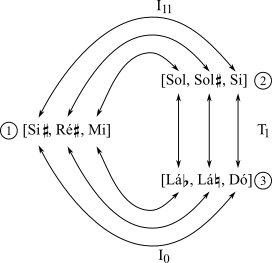
Para inverter um conjunto, simplesmente inverta cada número do conjunto um por um (Exemplo 2-12).

Note-se que as formas normais de conjuntos relacionados por inversão são imagens espelhadas um do outro: a primeira nota de um comjunto corresponde à última nota do outro, a segunda à penúltima e, assim por diante.
Linhas relacionadas por inversão tem o contorno oposto (o que sobe por alguma quantidade numa linha desce pela mesma quantidade na outra) e, cada par de notas correspondentes tem a mesma soma.
Quando X é invertido em Y à In (X e Y podem ser linhas ou conjuntos de notas ou classes de notas), cada cn x em X é invertida em uma cn correspondente y em Y, tal que x + y = n. X e Y compartilham os mesmos intervalos, mas na direção contrária.
2.5 Inversão (Ixy).
Há outra maneira de falar sobre inversão: Ixy, onde x e y são classes de notas que se invertem uma na outra (x e y podem ser quaisquer classes de notas e podem ser a mesma classe de notas). Ao especificar qualquer par mapeado, simultaneamente especifica-se todos os outros.
Há doze inversões possíveis, cada qual resultando num conjunto único de mapeamentos (Figura 2-8 a seguir). Para cada inversão, os mapeamentos estão indicados com linhas curvas no mostrador de relógio de classes de notas e, os possíveis rótulos na forma Ixy estão listados abaixo. É fácil trasladar do modelo Ixy para o modelo In de inversão porque x + y = n. Para encontrar o número de índice relevante, simplesmente some qualquer par de notas. O número de índice para cada uma das doze inversões está dado acima dos mostradores de relógio.
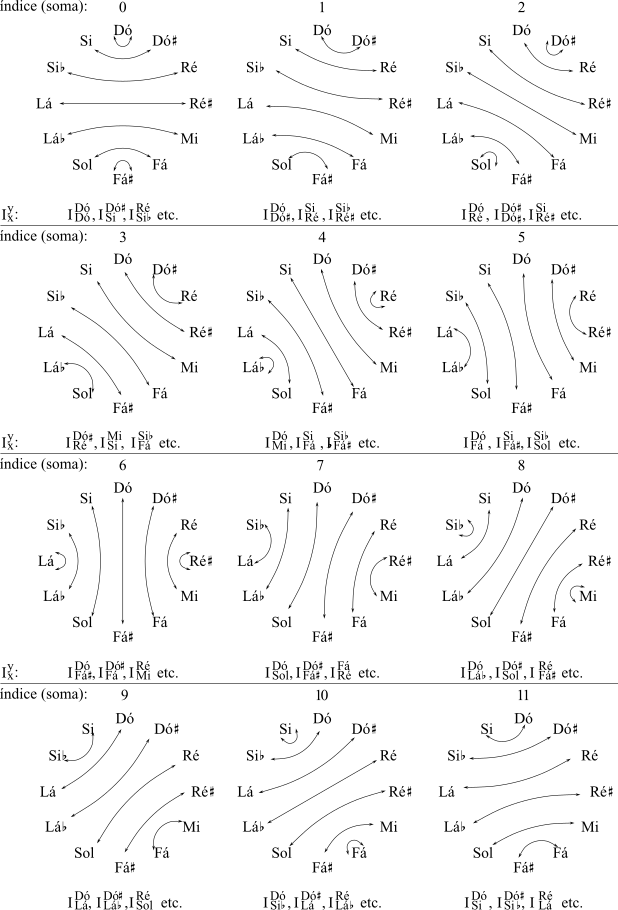
A inversão envolve pares de notas que compartilham um índice de inversão (soma).
2.6 Classes de conjuntos.
Considere a coleção de conjuntos de classes de notas em forma normal mostrada no Quadro 2-2 a seguir. A primeira coluna começa com um conjunto escolhido arbitrariamente que é então transposto a cada um dos outros onze níveis de transposição. Assim, cada um dos doze conjuntos está relacionado aos onze remanescentes por transposição. A segunda coluna começa com uma inversão do conjunto e então o transpõe sistematicamente. Na segunda coluna como na primeira, cada conjunto de classes de notas está relacionado por transposição aos outros onze. Os conjuntos dentro de cada coluna são às vezes referidos como definindo um Tipo-Tn. Um Tipo-Tn é uma classe de conjuntos que estão todos relacionados por transposição. Normalmente um Tipo-Tn contém doze diferentes conjuntos. As doze tríades menores, por exemplo, compreendem um único Tipo-Tn, assim como os doze acordes de sétima da dominante.
Considerando-se todos os vinte e quatro conjuntos juntos, dentro de cada coluna, os conjuntos estão todos relacionados por transposição. Ao mesmo tempo, cada conjunto em uma coluna está relacionado por inversão com os conjuntos na outra coluna. Assim, cada um dos vinte e quatro conjuntos está relacionado com todos os outros tanto por inversão quanto por transposição. Eles formam uma família única, intimamente relacionada de conjuntos. Uma família como essa é chamada de classe de conjuntos (também referida como uma classe de conjunto T/I).
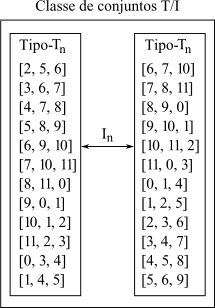
Normalmente, uma classe de conjuntos contém vinte e quatro membros. Algumas, entretanto, tem menos de vinte e quatro membros. Por exemplo, o acorde de sétima diminuta. Ao escrevê-lo começando cada vez em cada uma das doze classes de notas e então invertê-los fazendo o mesmo, rapidamente notaremos uma grande quantidade de duplicações. Ao eliminar todas as duplicações, vê-se que esta classe de conjuntos específica contém somente três membros distintos. Poucos conjuntos são tão redundantes quanto esse (embora um conjunto, a escala de tons inteiros, seja ainda mais).
A agregação de classes de conjuntos é uma parte importante da estrutura musical pós-tonal. Há literalmente milhares de conjuntos de classes de notas, mas uma quantidade muito menor de classes de conjuntos. Cada conjunto de classes de notas pertence a uma única classe de conjuntos. Os conjuntos em uma classe de conjuntos estão todos relacionados ou por Tn ou In. Como resultado, eles todos têm o mesmo conteúdo classe-intervalar.
Movendo-se de conjunto em conjunto dentro de uma única classe de conjuntos, um compositor pode criar um senso de coerência e de movimento musical direcionado. Ver o Exemplo 2-13 ao lado. A análise de rede do excerto está a seguir na Figura 2-9.
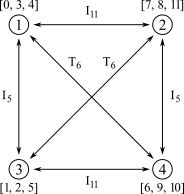
Há muitas ocorrências de outros membros da mesma classe de conjuntos nessa passagem. Ela está saturada com ocorrências de membros dessa classe. Ele ocorre como um fragmento melódico, como um acorde e como uma combinação de melodia e acorde. Ele está articulado por registro e, em grande escala, por contorno. Uma rede inteira de associações musicais irradia da figura melódica de três notas inicial. Algumas das aparições posteriores tem o mesmo conteúdo de notas, outras o mesmo conteúdo de classes de notas. Algumas estão relacionadas por transposição, outras por inversão. Todas são membros da mesma classe de conjuntos. Como na música tonal, mas com intensidade ainda maior, uma ideia musical inicial cresce e se desenvolve conforme a música progride. A mera presença de muitos membros de uma única classe de conjuntos garante um certo tipo de unidade sonora. Mas geralmente há mais interesse nos meios pelos quais a música se move de um conjunto para outro dentro de uma classe de conjuntos do que no simples fato de pertencer à uma classe de conjuntos.
Uma classe de conjuntos é uma coleção de conjuntos de classes de notas relacionadas tanto por T quanto por I
2.7 Forma prima.
Classes de conjuntos são identificadas pela sua forma prima, uma representação que começa com 0 e é mais compacta à esquerda. Por exemplo, dos membros da classe de conjuntos mostrados no Exemplo 2u, dois começam com 0: (034) e (014). Destes, (014) é mais compacto à esquerda e é, portanto, a forma prima. Aqueles vinte e quatro conjuntos são todos membros da classe de conjuntos com forma prima (014). Usando cc como abreviatura para classe de conjuntos, diz-se que cada um daqueles conjuntos é um membro da cc(014) ou, mais familiarmente que, cada um deles “é um (014)”. As formas primas são escritas entre parênteses sem vírgulas separando os elementos. As letras A e B representarão 10 e 11 neste formato compacto (*).
Para identificar a classe de conjuntos à qual algum conjunto de classes de notas pertence, tem-se que pôr o conjunto em forma prima. O Quadro 2-3 a seguir mostra o procedimento passo-a-passo com alguns exemplos ilustrativos.
Quadro 2-3: pondo conjuntos em forma prima.
| Procedimento | Exemplo 1 | Exemplo 2 | Exemplo 3 |
|---|---|---|---|
Começar com um conjunto em forma normal. | [Dó#, Fá, Fá#, Sol] | [Sib, Ré, Fá, Fá#] | [Fá, Fá#, Lá] |
| Extrair a sucessão de intervalos. | 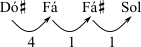 | 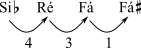 | 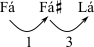 |
Escolher a sucessão de intervalos lendo da esquerda para a direita e da direita para a esquerda, qualquer que tenha os menores intervalos em direção à esquerda. | 1 - 1 - 4 é mais compacto à esquerda do que 4 - 1 - 1. | 1 - 3 - 4 é mais compacto à esquerda do que 4 - 3 - 1. | 1 - 3 é mais compacto à esquerda do que 3 - 1. |
| Extrair a sucessão de intervalos. | 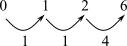 Forma prima = (0126) | 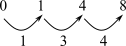 Forma prima = (0148) | 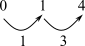 Forma prima = (014) |
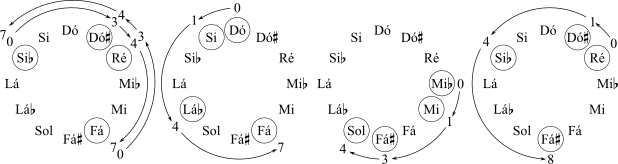
Assim como com a forma normal, geralmente é possível determinar a forma prima simplesmente inspecionando um conjunto disposto no mostrador de relógio de classes de notas. Encontra-se a maior lacuna entre as classes de notas. Designa-se zero à nota no final da lacuna e leia-se uma possível forma prima no sentido horário. Depois designa-se zero à nota no início da lacuna e leia-se outra possível forma prima no sentido anti-horário. (Se houver duas lacunas do mesmo tamanho, escolhe-se aquela que tiver outra lacuna relativamente grande próxima dela.) Qualquer dessas formas primas potenciais que tiver menos inteiros grandes é a verdadeira forma prima. Se estiver em dúvida, consulte a Lista de Classes de Conjuntos nesse apontador: todas as formas primas estão listadas lá.
A Figura 2-10 ilustra o uso do mostrador de relógio de classes de notas com os quatro exemplos usados para determinar a forma normal. Observe-se que o primeiro dos quatro conjuntos tem os mesmos intervalos lendo de baixo para cima quanto de cima para baixo. Isso acontece porque eles são inversivamente simétricos, um conceito que será estudado mais adiante. Descobrir a forma prima e basicamente uma questão de visualização e ficará mais fácil com a prática.
A forma prima é uma maneira simples de identificar uma classe de conjuntos como uma linha de inteiros de classes de notas começando em 0.
2.8 Lista de classses de conjuntos.
Nesse apontador, encontra-se uma Lista de Classes de Conjuntos. Note quão poucas classes de conjuntos há. Com as nossas doze classes de notas, é possível construir 220 tricordes (conjuntos de três membros). Entretanto, esses tricordes distintos podem ser agrupados em apenas doze classes de conjuntos tricordais diferentes na Lista de Classes de Conjuntos. Semelhantemente, há somente vinte e nove classes de tetracordes (conjuntos de quatro membros), trinta e oito classes de pentacordes (conjuntos de cinco membros) e, cinquenta classes de hexacordes (conjuntos de seis membros). A discussão de conjuntos com mais de seis elementos está na próxima unidade.
A Lista das Classes de Conjuntos está construída de modo a tornar uma grande quantidade de informações úteis prontamente disponíveis. Na primeira coluna, há uma lista de formas primas, dispostas em ordem ascendente. A segunda coluna dá o assim chamado “nome de Forte” para cada classe de conjuntos. Allen Forte, que foi o pioneiro da teoria dos conjuntos de classes de notas, identificou as classes de conjuntos com um par de números separados por um traço. O primeiro número diz a quantidade de classes de notas no conjunto (sua cardinalidade); o segunda dá a posição do conjunto na lista de Forte. A classe de conjuntos 3-4, por exemplo, é o quarto conjunto na lista de Forte dos conjuntos de três notas. Em geral far-se-á referência às classes de conjuntos pela sua forma prima, mas ocasionalmente usar-se-á o nome de Forte também.
A terceira coluna contém o vetor classe–intervalar para a classe de conjuntos. (Esse é o vetor classe–intervalar para cada membro da classe de conjuntos, já que o conteúdo intervalar não muda sob transposição ou inversão.) Na quarta coluna estão dois números separados por uma vírgula; esses números mensuram a simetria transpositiva e inversiva da classe de conjuntos (esses conceitos serão discutidos na próxima unidade). Lado a lado com cada tricorde, tetracorde, e pentacorde, e alguns dos hexacordes, está outro conjunto com todas as suas informações relevantes em ordem reversa. A discussão sobre esses hexacordes, septacordes, octacordes e nonacordes está também na próxima unidade. A Lista de Classes de Conjuntos provê ainda nomes comuns para algumas dessas classes de conjuntos.
A Lista de Classes de Conjuntos identifica a forma prima e o vetor classe-intervalar de cada classe de conjuntos
2.9 Segmentação e análise.
Na música pós-tonal discutida aqui, a coerência é frequentemente criada pelos relacionamentos entre conjuntos dentro de uma classe de conjuntos. É possível ouvir caminhos através da música conforme um ou mais conjuntos são transpostos e invertidos de maneiras intencionais e direcionadas. Frequentemente, percebe-se que não há apenas um único e melhor meio para ouvir nosso caminho através de uma peça; mais que isso, a audição frequentemente necessita ser múltipla, conforme os diferentes caminhos se intersectam, divergem, ou correm paralelos uns aos outros. Para usar uma metáfora diferente, a música pós-tonal é muitas vezes semelhante a um tecido rico e variado, composto de muitos fios diferentes. Conforme tenta-se compreender a música, a tarefa é desfiar os fios para inspeção, e então ver como eles se combinam para criar o tecido maior.
Uma das principais tarefas analíticas, então, é encontrar os conjuntos principais e mostrar como eles estão transpostos e invertidos. Mas como saber quais conjuntos são os importantes? A resposta é que não pode saber com antecedência. Deve-se entrar no mundo da peça – ouvindo, tocando, e cantando – até que se obtenha um senso de quais ideias musicais são fundamentais e recorrentes. No processo, move-se em torno de um tipo familiar de círculo conceitual. Não se pode saber quais são as principais ideias até que se as veja recorrer; mas não pode encontrar recorrências até que se saiba quais são as ideias principais. A única solução prática é bisbilhotar a peça, propondo e testando hipóteses conforme se prossegue. No processo, pode-se considerar muitas segmentações diferentes da música, isto é, maneiras de esculpi-la em agrupamentos musicais cheios de significado.
Quando se identifica o que se pensa ser uma ideia musical significativa, então procura-se cuidadosa, completa, e imaginativamente por suas recorrências transpostas ou invertidas. Aqui estão alguns lugares para procurar (esta lista não é exaustiva!):
- Numa linha melódica, considera-se todos os segmentos melódicos. Por exemplo, se a melodia tem seis notas, então as notas 1–2–3, 2–3–4, 3–4–5 e 4–5–6 são todas agrupamentos de três notas viáveis. Esse jeito sistemático de agrupar notas é às vezes chamado de imbricação. Alguns desses agrupamentos podem estender-se sobre pausas ou limites frasais, e isso está bem. Uma rica interação entre estrutura de frase e estrutura de classes de conjuntos é uma característica familiar da música pós-tonal.
- Harmonicamente, a busca não deve se restringir apenas a acordes onde todas as notas são atacadas ao mesmo tempo. Mais do que isso, deve-se considerar todas as simultaneidades, isto é, as notas soando simultaneamente a cada ponto específico. Há que mover-se através da música como um cursor sobre uma página, considerando todas as notas soando a cada momento.
- As notas podem estar associadas por registro. Numa melodia ou frase, considere as notas mais agudas (ou mais graves), ou os pontos agudos (ou graves) de frases sucessivas.
- As notas podem estar associadas ritmicamente de várias maneiras. Considera-se como um agrupamento possível as notas ouvidas em tempos fortes sucessivos, ou as notas ouvidas no início de uma figura rítmica recorrente, ou as notas às quais são dadas as maiores durações.
- As notas podem estar associadas timbristicamente de várias maneiras. Considere como um grupo possível as notas que são produzidas por algum meio distinto, por exemplo, por um único instrumento em um conjunto, ou por certo tipo de articulação (e.g., staccato, pizzicato).
Em todas as segmentações musicais, há que esforçar-se para obter um equilíbrio entre busca imaginativa e bom senso musical. Por um lado, não se restringir aos agrupamentos óbvios (embora esses sejam um bom lugar para começar). Relações interessantes podem não estar aparentes na primeira, segunda, ou terceira vez, e precisa-se ser exaustivo e persistente nas investigações. Por outro lado, deve-se ficar dentro dos limites do que pode ser significativamente ouvido. Não pode pinçar notas de maneira aleatória, só porque elas formam um conjunto no qual se está interessado. Mais ainda, as notas que se agrupa devem estar associadas umas com as outras de alguma maneira musical. Elas devem compartilhar alguma qualidade distintiva (por exemplo, de proximidade, ou culminância, ou tessitura, ou intensidade, ou duração) que as agrupe e as distinga das notas em torno delas. Se, após alguns repetidos esforços de boa-fé para ouvir certo agrupamento musical, não se puder torná-lo realmente palpável, então se o abandone e se vai para a próxima coisa. O objetivo é descrever a rede de relações musicais mais rica possível, para deixar nossas mentes e ouvidos musicais guiarem-se uns aos outros com os muitos caminhos agradáveis através dessa música.
Ao analisar música pós-tonal, deve-se sentir-se livre para esgotar a faixa inteira de conceitos desenvolvidos nas Unidades 1 e 2 desse material, desde o mais concreto até o mais abstrato (ver o Quadro 2-4 a seguir).
Quadro 2-4: uma variedade de conceitos teóricos, do mais concreto ao mais abstrato.
Notas → Classes de notas
Intervalos de notas → Intervalos ordenados de classes de notas → Classes de intervalos
Conjuntos de classes de notas → Tipos-Tn → Classes de conjuntos (Classes de conjuntos T/I)
No processo, pode-se descobrir o quão difícil é encontrar explicações para cada nota numa peça ou mesmo numa curta passagem. Uma característica familiar dessa música é sua resistência a explicações simples e abrangentes. Em vez de tentar encontrar uma fonte única para toda a música, deve-se tentar forjar redes significativas de relacionamentos, retirando fios particularmente notáveis do tecido musical, e seguindo uns poucos caminhos musicais interessantes. Esse é um objetivo atingível e satisfatório para a análise musical e para a audição musical.
A análise pode envolver a identificação de conjuntos de classes de notas importantes e relacioná-los uns com os outros via T ou I.
