Introdução à teoria pós-tonal (4a. ed.).

6. Conceitos básicos de música dodecafônica.

6.1 Séries dodecafônicas.

6.1.1 Conjuntos e séries.

Até aqui se discutiu música amplamente em termos de conjuntos não ordenados de classes de notas. A seguir, concentra-se em conjuntos ordenados os quais serão chamados de séries. Uma série é uma linha de classes de notas. Um conjunto de classes de notas retém sua identidade não importa como as suas classes de notas sejam ordenadas. Numa série, entretanto, as classes de notas ocorrem numa ordem específica; a identidade da sértie muda se a ordem muda. Uma série (às vezes chamada de fila) pode ter qualquer tamanho, mas de longe a mais comum é uma série consistindo em todas as doze classes de notas (uma de cada). Música que usa uma tal série como sua estrutura referencial básica é conhecida como música dodecafônica [*].

6.1.2 O papel da série.

Uma série dodecafônica desempenha muitos papéis musicais na música dodecafônica. De certa forma ela é como um tema, uma "melodia" reconhecível que recorre de várias formas através da peça. De certa forma ela é como uma escala, a coleção referencial básica da qual harmonias e melodias são extraídas. De certa forma ela é um repositório de motivos, um grande modelo dentro do qual estão embutidos numerosos modelos menores. Mas ela desempenha um papel mais fundamental na música dodecafônica do que um tema, uma escala ou um motivo desempenham na música tonal. Na música tonal as escalas, e mesmo em alguma extensão os temas e os motivos, são parte de uma propriedade comum do estilo musical prevalente. De peça para peça, de compositor para compositor, uma grande quantidade de material musical é compartilhada. A música tonal é relativamente comunal. Na música dodecafônica, entretanto, relativamente pouco é compartilhado de peça para peça ou de compositor para compositor; virtualmente duas peças não compartilham a mesma série. A música dodecafônica é assim relativamente contextual. A série é a fonte de relações estruturais numa peça dodecafônica: da superfície imediata ao nível estrutural mais profundo a série molda a música.

A série é uma linha (sucessão ordenada) de classes de notas. O tipo mais comum de série contém uma de cada uma das doze classes de notas.

6.2 Operações básicas.

6.2.1 Conteúdo e ordem.

Como os conjuntos ordenados de classes de notas, as séries dodecafônicas podem ser submetidas a várias operações como transposição e inversão para fins de desenvolvimento, contraste e continuidade. Entretanto, há uma diferença básica importante. Quando um conjunto com menos de doze elementos é transposto ou invertido, o conteúdo do conjunto geralmente muda. Quando qualquer membro de (0123), por exemplo, é transposto dois semitons mais agudo, duas novas classes de notas são introduzidas. A operação de transposição, portanto, muda o conteúdo da coleção. Quando uma série dodecafônica é transposta, entretanto, o conteúdo permanece o mesmo. Ao se transpor as doze classes de notas, obtém-se apenas as mesmas classes de notas, mas numa ordem diferente. O mesmo é verdade para a inversão. No sistema dodecafônico, as operações básicas - transposição e inversão - afetam a ordem, não o conteúdo.

6.2.2 Ordem original [*].

As séries são tradicionalmente usadas em quatro ordens diferentes: original, retrógrada, inversa e retroinversa [**]. Alguma apresentação da série, geralmente a primeira da peça, é designada de original e as restantes são calculadas em relação a ela. No Exemplo 6-1, a melodia [...] apresenta todas as doze classes de notas de maneira clara e direta. Considera-se esta a ordem original da peça. Ela começa com Ré (classe de notas 2), portanto, será rotulada de O₂. As doze notas de O₂ são numeradas por ordem de ocorrência de 1 a 12.

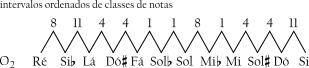
Pelo fato de se estar lidando com sucessões ordenadas de classes de notas, quando se fala sobre intervalos, fala-se fazendo referência aos intervalos ordenados de classes de notas. Estes são geralmente representados como números inteiros positivos de 1 a 11, mas às vezes se pode usar números negativos para o 7 e acima (7 = -5, 8 = -4, 9 = -3, 10 = -2 e 11 = -1). O Exemplo 6-2 mostra os onze intervalos ordenados de classes de notas da série.

6.2.3 Transposição.

Veja-se o que acontece com os intervalos ao transpor O₂ sete semitons acima (Exemplo 6-3).

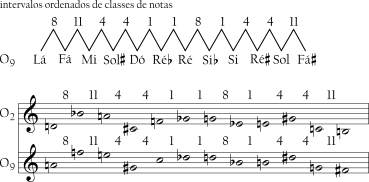
A ordem das classes de notas muda: o Ré era o primeiro, agora está perto do final; o Lá era o terceiro, agora é o primeiro e assim por diante. De fato, nenhuma classe de notas ocupa a mesma ordem de posição que ocupava. O conteúdo, obviamente, é o mesmo (tanto O₂ quanto O₇ contém todas as doze classes de notas) e, mais importante, também a sucessão de intervalos é a mesma. Aquela sucessão específica de intervalos é o que define a ordem original da série. Pode-se produzir aquela sucessão começando em qualquer das doze classes de notas. O₀ é a ordem original começando com a classe de notas 0; O₁ é a ordem original começando com a classe de notas 1 e assim por diante. Há doze formas diferentes da ordem original: O₀, O₁, O₂, ..., O₁₁.

6.2.4 Retrógrada.

Assim como com as outras ordenações (retrógrada, inversa e retroinversa), pode-se pensar nelas em termos de seu efeito sobre as classes de notas ou o seu efeito sobre os intervalos. Em termos de de classes de notas, a retrógrada simplesmente reverte a ordem original. O que acontece com a sucessão de intervalos quando O₂ é tocada de trás para a frente (uma ordem chamada R₂)? O Exemplo 6-4 demonstra.

A sucessão de intervalos é revertida e cada intervalo é substituído pelo seu complemento mod 12 (1 torna-se 11, 2 torna-se 10 etc.). Assim como com a ordem original, há doze formas diferentes de ordenamentos retrógrados: R₀, R₁, R₂, ..., R₁₁. (Lembrar-se de que R₀ é a retrógrada de O₀, R₁ é a retrógrada de O₁ e assim por diante. R₀ portanto, termina em vez de começar com 0.)

6.2.5 Invertida.

A invertida da série envolve a inversão de cada uma das classes de notas da série: ) inverte-se em 0, 1 inverte-se em 11, 2 inverte-se em 10, 3 inverte-se em 9 e assim por diante. O Exemplo 6-5 mostra a sucessão de intervalos para I₇, a ordem invertida que começa com a classe de notas 7. (observe-se que se está usando agora I_n como o nome para a série, ao passo que previamente se o usava somente como uma operação para conectar dois conjuntos. Estes significados diferentes, mas relacionados, normalmente ficam claros pelo contexto.)

A sucessão de intervalos aqui é a mesma daquela da ordem original, mas cada intervalo é substituído pelo seu complemento mod 12. Os intervalos são os mesmos que os da retrógrada, mas na ordem reversa. Como com as ordens original e retrógrada, pode-se reproduzir esta sucessão de intervalos começando em qualquer das doze classes de notas. AS doze séries resultantes serão chamadas I₀, I₁, I₂, ..., I₁₁.

6.2.6 Retroinvertida

A retroinvertida da série é simplesmente a retrógrada da invertida. O Exemplo 6-6 mostra a sucessão de intervalos para RI₇ (I₇ tocada de trás para frente.)

A sucessão intervalar aqui é similar àquela das outras três transformações É particularmente interessante compará-la com a da ordem original. Em termos de classes de notas as duas ordens parecem afastadas: cada uma é a versão de cabeça para baixo e de trás para a frente da outra. Em termos de intervalos, entretanto, as duas são muito similares: elas têm os mesmos intervalos na ordem reversa. Comparada com a retrógrada, a retroinvertida têm os intervalos complementares de trás para a frente. Assim como com as outras três transformações, a retroinvertida pode começar em qualquer das doze classes de notas. As formas da série resultantes são chamadas de RI₀ (a retrograda de I₀, RI₁ (a retrógrada de I₁, ..., RI₁₁ (a retrógrada de I₁₁).

6.2.7 Classe de séries (classe de filas).

Para qualquer série tem-se assim uma família de quarenta e oito formas de séries: doze originais, doze retrógradas, 12 invertidas e doze retroinvertidas. Aquela família de formas de séries é conhecida como classe de séries (ou classe de filas). As séries na classe de séries estão todas relacionadas por T, R, I ou RI e cada série individual é um membro (representante) da classe. Todos os membros da classe de séries estão intimamente relacionados tanto pelas classes de notas quanto pelos intervalos.

O Quadro 6-1 mostra os intervalos descritos pelos quatro ordenamentos diferentes da série [...].

Quadro 6-1: intervalos dos quatro ordenamentos da série [...].

Intervalos ordenados de classes de notas
Original	8	11	4	4	1	1	8	1	4	4	11
Retrógrada	1	8	8	11	4	11	11	8	8	1	4
Invertida	4	1	8	8	11	11	4	11	8	8	1
Retroinvertida	11	4	4	1	8	1	1	4	4	11	8

Observe-se a predominância dos intervalos 1, 4, 8 e 11 e a completa exclusão de 3 e 9 [e outros] nos quatro ordenamentos (e assim em todas as quarenta e oito séries da classe de séries). Por causa dessas características intervalares compartilhadas (e muitas outras características a serem discutidas mais tarde), as formas de uma série estão intimamente relacionadas umas com as outras. Cada uma delas pode transmitir a uma peça a mesma sonoridade distintiva.

A Figura 6-1 resume as relações intervalares entre as formas da série.

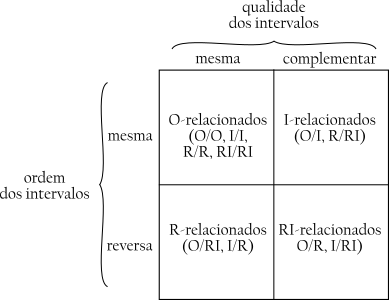
As séries que tem o mesmo ordenamento (O e O, I e I, R e R ou RI e RI) são ditas original-relacionadas e têm os mesmos intervalos na mesma ordem. Séries que estão relacionadas por inversão (O e I, R e RI) têm os intervalos complementares na mesma ordem. Séries que estão relacionadas por retroinversão (O e RI, I e R) têm os mesmos intervalos na ordem reversa. Séries que são retrógrado-relacionadas (O e R, I e RI) têm os intervalos complementares na ordem reversa.

6.2.8 A matriz 12 x 12.

Ao estudar uma peça dodecafônica é conveniente ter à mão uma lista de todas as quarenta e oito formas da série. Pode-se simplesmente escrever todas as quarenta o oito tanto numa pauta musical quanto usando inteiros de classes de notas. Mais simplesmente, pode-se escrever as doze originais e as doze invertidas (usando a pauta musical, nomes de [notas com] letras, ou inteiros de classes de notas) e simplesmente encontrar as retrógradas e retroinvertidas lendo-as de trás para a frente. O meio mais simples de todos, entretanto, é construir o que é conhecido como uma matriz 12 x 12.

Para construir uma tal matriz, começa-se escrevendo O₀ horizontalmente na parte superior e I₀ abaixo no lado esquerdo (ver o Quadro 6-2).

Depois escreve-se as ordens originais remanescentes nas filas da esquerda para a direita, começando em qualquer classe de notas que esteja na primeira coluna. A segunda fila conterá O₄, a terceira fila conterá O₅ e assim por diante (ver o Quadro 6-3).

As filas da matriz, lendo da esquerda para a direita, contém todas as formas originais e lendo da direita para a esquerda as formas retrógradas. As colunas da matriz lendo de cima para baixo contém todas as formas invertidas e de baixo para cima as formas retroinvertidas. A mesma matriz pode ser escrita usando letras de nomes [de notas] em vez de inteiros de classes de notas.

A matriz assim contém a classe de série inteira: uma pequena e coerente família de quarenta e oito formas da série intimamente relacionadas (doze originais, doze retrógradas, doze invertidas e doze retroinvertidas). Todo o material de notas essencial numa peça dodecafônica é normalmente extraído dessas quarenta e oito formas. Na verdade, muitas peças dodecafônicas usam bem menos do que quarenta e oito formas diferentes. O material, portanto, é estritamente circunscrito, mas ainda assim permite muitos tipos diferentes de desenvolvimento. Um compositor constrói a partir da série (e, portanto, a partir da família inteira de quarenta e oito formas) certos tipos de estruturas e relações. Um compositor baseado naquela série ode expressar aquelas estruturas e relações de muitas maneiras diferentes.

6.2.9 A "contagem das doze".

Uma boa maneira de se orientar numa obra dodecafônica é pela identificação das formas das séries conhecida como contagem das doze. Isoo pode prover um tipo de mapa de baixo nível de uma composição. O primeiro asso na contagem das doze é identificar a série. Ela geralmente é apresentada de algum modo explícito bem no início da peça, mas às vezes um pouco de trabalho de detetive é necessário. Por exemplo [...] a melodiada passagem [...] apresenta a série dodecafônica da peça e então, repete as cinco primeiras notas (Exemplo 6-7) [**].

Designa-se aquela forma da série de O porque ela é proeminente e fácil de seguir. Observe-se o procedimento comum de contagem das doze para identificar a posição de ordem que cada nota ocupa na forma da série (Ré é a primeira, Si é a segunda e assim por diante).

Agora o problema é identificar as formas da série usadas no acompanhamento. Pode-se construir uma matriz 12 x 12, procurar as primeiras notas do acompanhamento (Fá, Mi, Lá, Dó) e ver qual das quarenta e oito formas começa assim. Mas também se pode encontrar a resposta mais diretamente aplicando o conhecimento das relaçoes intervalares entre as formas da série. Observe-se a sucessão de intervalos ordenados de classes de notas descrita por O₂ (Exemplo 6-8).

Agora olha-se aos intervalos ordenados de classes de notas descritos pelas primeiras cinco notas do acompanhamento (ver o Exemplo 6-9) [***].

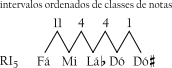
O acompanhamento começa com os mesmos intervalos com os quais O₂ termina, na ordem reversa. Isso significa que que se está lidando com uma forma RI. A qual nível de transposição? Simplesmente adiciona-se a primeira nota do acompanhamento (Fá ou 5) com a última nota de O₂ (Si, 11), a segunda nota do acompanhamento (Mi, 4) com a penúltima nota de O₂ (Dó, 0) e assim por diante. Dessa forma, calcula-se o número de índice que mapeia essas séries uma na outra. A soma em cada caso é 4, assim, as duas formas da série estão relacionads à I₄. A forma da série da melodia é O₂, portanto a forma da série do acompanhamento deve ser RI₂, porque 2 + 2 = 4. Se duas séries estão relacionadas à I₄ o eixo de inversão será Ré—Sol, e nesta música o Ré em particular desempenha o papel de centro de simetria inversiva.

Essa passagem usa apenas O₂ e RI₂[...] (Exemplo 6-10).

Observe-se que uma nota pode ser simultaneamente a última nota de uma forma da série e a primeira da próxima. O Ré no acompanhamento no compasso 2, por exemplo, é tanto a última nota de RI₂ quanto a primeira nota de O₂. Esse tipo de superposição é típico de Webern. Uma contagem das doze como essa não ajuda a ouvir a peça melhor - as relações intervalares discutidas no Capítulo 1 são provavelmente mais úteis para isso - mas ela dá um esboço estrutural aproximado da peça. Ela também fornece um contexto mais esclarecido para aquelas relações intervalares.

6.2.10 Compondo com uma série.

Não há nada mecânico nem sobre a construção de uma série nem quanto ao seu desenvolvimento musical em uma composição. A um compositor de música tonal certos materiais são dados para trabalhar, incluindo mais obviamente escalas diatônicas e tríades maiores e menores. O compositor de música dodecafônica deve construir os seus próprios materiais básicos. embutindo-os dentro da série. Quando chaga a hora de usar aqueles materiais básicos numa peça de música, um compositor dodecafônico, assim como um compositor tonal, o faz de maneira que lhe pareça musical e expressivamente mais conveniente Um bom compositor não se limita a encadear séries musicais, assim como Mozart não se limita a simplesmente amarrar escalas.

Uma vez que uma série esteja construída, um processo que será descrito posteriormente, pode-se pensar em quantas decisões compositivas ainda serão requeridas para torná-la música. Deverão as notas soar uma de cada vez ou algumas delas deverão ser ouvidas simultaneamente? Em quais registros elas devem ocorrer? Tocadas por quais instrumentos? Com quais durações? Quais articulações? É como receber escala de Dó maior e ter que compor alguma música. Há certas restrições, mas também muita liberdade

[...] O Exemplo 6-11 mostra duas outras apresentações de O₂, ambas da seção inicial da peça [*].

A ideia musical é reconhecível em cada caso, mas admiravelmente variada. Como Schoenberg disse, a música geralmente envolve remodelamento sem fim de um modelo básico. A construção da série, a escolha das formas da série, e mais importante, a apresentação das séries, são decisões musicais baseadas em relações musicais audíveis.

Uma série pode ser apresentada em quatro ordenações: original, retrógrada, invertida e retroinvertida. As transposições dessas ordenações formam uma classe de séries (ou classe de filas), que constitui um ponto de partida para composições musicais.

6.3 Subconjuntos segmentados.

Uma série é construída a partir de suas partes menores, seus subconjuntos. A sonoridade de uma série, e portanto, a sonoridade de uma peça baseada na série, é moldada pela estrutura de seus subconjuntos. Já se mencionou as díades (intervalos) formados por notas adjacentes. É possível construir séries com características intervalares muito diferentes. Webern, por exemplo, preferia séries que usam uns poucos intervalos diferentes e que fazem uso maciço da classe de intervalos 1. Berg, em contraste, tinha preferência por séries que usam intervalos triádicos, classes de intervalos 3, 4 e 5. De modo grosseiro, aquelas preferências contrastantes explicam a diferença de sonoridade na música dodecafônica de Webern e Berg.

Além das díades, pode-se considerar subconjuntos de qualquer tamanho, mas os de três, quatro e seis elementos são geralmente os mais importantes. Os compositores tendem a embutir na série os conjuntos menores que estão interessados em usar. Colocando de outra forma, eles geralmente constroem suas séries pela combinação de uma quantidade de conjuntos menores. Como ouvintes, muitos acham difícil compreender uma série como um todo e que é quase impossível reconhecer quando uma série está virada de cabeça para baixo e de trás para a frente, por exemplo. Felizmente, muita música dodecafônica não requer que as pessoas sejam capazes de ouvi-la daquela maneira. Em vez disso, tudo o que se tem que ouvir são coleções menores, os intervalos e subconjuntos embutidos na série.

Lembre-se de que cada forma da uma série terá a mesma estrutura de subconjuntos. Se, por exemplo, as três primeiras notas de O₀ forem membros da cc(027), então também serão as três primeiras notas de todas as formas O e formas I, e as três últimas notas das formas R e formas RI. Isso porque a associação com uma classe de conjuntos não é afetada por transposição, inversão ou retrogradação.

6.3.1 Apresentação direta.

Continuando o estudo do Quarteto de Cordas No. 4 de Schoenberg. O Exemplo 6-12 [*] identifica uma quantidade de subconjuntos segmentados da série, isto é, grupos de classes de notas que são contíguos dentro da série.

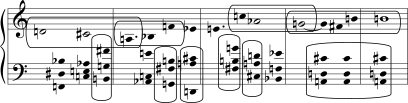
Os conjuntos sobre colchetes e as classes de conjuntos que eles representam são motivos recorrentes importantes na música. O tricorde (015), por exemplo, ocorre muitas vezes dentro da série. No início do quarteto (Exemplo 6-13 [**]), a música divide a série em seus quatro tricordes discretos. (Subconjuntos discretos são aqueles que dividem a série em porções não sobrepostas. Há quatro tricordes discretos [Exemplo 6-12a], três tetracordes discretos [Exemplo 6-12c] e dois hexacordes discretos em todas as séries.) Cada tricorde da melodia está acompanhado pelos três tricordes restantes nos outros instrumentos. Enquanto o pri9meiro violino toca o primeiro tricorde (Ré-Dó-Lá), os instrumentos remanescentes tocam o segundo (Si-Fá-Ré), terceiro (Mi-Dó-Lá) e o quarto (Sol-Fá-Si); quando o primeiro violino toca o segundo tricorde os outros instrumentos tocam o primeiro, o terceiro e o quarto e assim por diante. Cada tricorde, portanto, ocorre quatro vezes na passagem, uma vez na melodia e três vezes no acompanhamento. Como dois dos tricordes discretos são (015) e, como aquela classe de conjuntos também ocorre em dois outros lugares na série, a passagem pode ser ouvida, em parte, como apresentações variadas daquela ideia musical.

6.3.2 Apresentação indireta.

Quanto aos tetracordes, foca-se agora a atenção em numa única classe de conjuntos: (0148) - ela ocorre três vezes na série (e, portanto, três vezes na melodia do primeiro violino nos compassos 1 a 6.) - ver o Exemplo 6-12d. Viu-se que essa passagem envolve uma melodia acompanhada por acordes de três notas. Mas como Schoenberg escolhe qual nota melódica soará com cada acorde? Nos compassos 1 a 6, por exemplo, porque o Dó melódico vem com o segundo acorde em vez de, diga-se, com o terceiro acorde? No compasso 2, o Lá melódico seria mais logicamente ouvido antes no compasso 1 com o terceiro acorde. Por que ele ocorre onde está?

Em ambos os casos a resposta parece ser que, com esse alinhamento vertical específico, Schoenberg é capaz de reproduzir classes de conjuntos que ocorrem como subconjuntos segmentados da série (Exemplo 6-14 [*]).

O Dó melódico e o segundo acorde do compasso 1 não são contíguos em O₂. Quando eles soam juntos, entretanto, eles criam uma forma de (0148), uma classe de conjuntos que sim, ocorre como um segmento linear da série. O mesmo acontece nos compassos 2 e 6. Esses alinhamentos verticais não são determinados pela série - eles resultam de escolhas compositivas independentes. Nesta peça, Schoenberg toma cuidado para que a dimensão linear e a relativamente livre dimensão vertical expressem as mesmas ideias musicais, ideias que estão embutidas na série. Desse modo, a série alcança uma influência ainda mais profunda na música.

Uma série é um repositório de ideias musicais: seus subconjuntos. Ao escrever uma série, um compositor escolhe intervalos, tricordes, tetracordes preferidos e assim por diante e os embute na série. Como compositores diferentes têm diferentes tipos de referências, as séries variam enormemente em suas características internas. É possível escrever séries que usam cada um os onze intervalos ordenados de classes de notas uma vez (chamadas série de "total intervalar" [**]) e séries que se confinam a somente um ou dois intervalos diferentes. É possível escrever séries nas quais cada um dos tricordes segmentados representam uma classe de conjuntos diferente (chamadas séries "toda tricordal" [**]) e séries nas quais todos os tricordes segmentados são do mesmo tipo. Em todos os casos, a estrutura de subconjuntos da série irá modelar profundamente a sonoridade e a estrutura de uma obra baseada nela.

Os subconjuntos segmentados de uma série (os menores conjuntos embutidos nela) são componentes harmônicos e motívicos audíveis da música dodecafônica.

6.4 Invariantes.

Quando se ouve música dodecafônica, não é necessário identificar as formas das séries. Ao invés, precisa-se ouvir as consequências musicais das séries, os resultados musicais de suas contínuas transformações. Qualquer qualidade ou relacionamento musical preservado quando uma série é transformada é chamado de uma invariante. Conforme se vai ouvindo uma peça, o ouvido frequentemente é conduzido via uma cadeia de invariantes.

Já se estudou ou se fez alusão a uma quantidade de invariantes musicalmente significativas. Por exemplo, observa-se que quando uma série é transposta, a sucessão dos intervalos permanece a mesma. Em outras palavras, a sucessão intervalar é mantida invariante sob transposição. Não é necessário ser capaz de identificar o nível ao qual a série foi transposta para ouvir que os mesmos intervalos estão voltando na mesma ordem. Também já foi discutida a estrutura de subconjuntos de uma série. Aquela estrutura permanece invariante sob inversão e transposição. Se todos os tricordes discretos de O₀ são membros de (014), por exemplo, então isso será verdadeiro para todas as quarenta e oito formas da série. Não importa como a série é transposta ou invertida ou retrogradada, sempre se será capaz de ouvira presença constante daqueles subconjuntos. Há tantos tipos diferentes de invariantes que seria impossível fazer um levantamento aqui. O que se fará ao invés será confinar a discussão às invariantes sob inversão e contentar-se com apenas duas instâncias específicas: a preservação de uma pequena coleção (díades ou tricordes) e manutenção de díades verticais em contraponto nota contra nota.

Para começar, lembre-se que a inversão sempre envolve um duplo mapeamento: se I_n mapeia x em y, então ela também mapeará y em x. Para dar um exemplo: I₅(1) = 4 e I₅(4) = 1. Pode-se usar essa relação não somente para classes de notas individuais, mas para coleções maiores também. Diga-se que há dentro de uma série um subconjunto (suas classes de notas reais, não só a sua classe de conjuntos) que se quer manter intacto (embora possivelmente reordenado) mesmo quando se o move para uma nova forma da série. Não é difícil fazê-lo, desde que haja um subconjunto equivalente, um relacionado por transposição ou inversão, em algum outro lugar da série. Se os dois subconjuntos estão relacionados por I_n, invertendo a série como um todo pela mesma I_n fará com que os dois subconjuntos se mapeiem um no outro, e ambos permanecerão intactos. Se os subconjuntos forem inversivamente simétricos, em algum nível de inversão eles permanecerão intactos pelo mapeamento em si mesmos.

6.4.1 Díades invariantes.

Os subconjuntos em questão podem ser tão pequenos quanto uma díade. No Exemplo 6-15 vê-se a série familiar do Quarteto de Cordas No. 4 de Schoenberg, escrita em inteiros de classes de notas e transposta para começar em Dó.

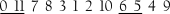
A série começa com a díade (0, 11). Se se quer manter 0 e 11 próximos um do outro enquanto se transforma a série, querer-se-á selecionar uma transformação que mapeará 0 e 11 neles mesmos ou em qualquer outra díade de semitom da série. Tenta-se [por exemplo] mapeá-la em (6, 5) (poder-se-ia facilmente escolher mapeá-la em qualquer dos outros semitons da série). Seria fácil fazer isso sob transposição, mas também é possível sob inversão. Procura-se pelo número de índice de [11, 0] e [5, 6]. O número de índice é 5 )0 + 5 = 6 + 11). I₅ portanto, mapeará 0 e 11 em 6 e 5 (e vice-versa). Compare-se O₀ com I₅ (ver o Exemplo 6-16).

A transformação de O₀ para I₅ move (0, 11) para o lugar inicialmente ocupado por (6, 5) e move (6, 5) para o lugar antes ocupado por (0, 11).

Schoenberg usa essa invariante para criar um caminho associativo através da música (Exemplo 6-17 [*]).

Em O₀ Dó-Si é a primeira coisa ouvida, enquanto Sol-Fá é a única díade repetida. A próxima forma da série é RI₅ (I₅ de trás para a frente). O Dó e o Si ainda estão juntos, agora repetidos (como Sol-Fá o foram antes), e o Sol e o Fá estão também juntos, agora no final da série. Conforme a música continua com R₀, Sol-Fá é tocada pelo violoncelo com os mesmos valores rítmicos e a apresentação de R₀ termina, obviamente, com Si-Dó. É difícil e musicalmente pouco recompensador ouvir a peça como uma O₀ seguida por uma RI₅ e por uma R₀. É mais fácil e musicalmente recompensador ouvir a cadeia de invariantes movendo-se através da música. A díade é a coleção mais simples de ouvir e discutir, mas os mesmos princípios se aplicam para manter coleções maiores invariantes também.

6.4.2 Tricordes invariantes.

Na série do Concerto para Violino de Berg, muitos dos subconjuntos segmentados são tríades maiores ou menores: Sol menor, Ré maior, Lá menor, Mi maior. Berg frequentemente produz uma sonoridade quase tonal nas suas obras dodecafônicas e esta série facilita fazê-lo. A série também contém duas ocorrências da tríade aumentada (048) e, como o Exemplo 6-17 mostra, estas se mapeiam uma na outro à I_2.

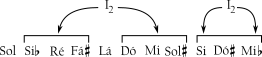
[Si, Dó, Mi], um membro da cc(024) ocorre mais adiante na série e mapeia-se em si mesma à I₂. Como resultado, ao se executar I₂ na série como um todo, as duas (048) mapear-se-ão uma na outra e (024) mapear-se-á em si mesma. Executar I₂ em O₇ produz I₇ porque 2 é o número de índice que relaciona as duas séries (7 + 7 = 2). O Exemplo 6-18 compara O₇ e I₇ e mostra a invariância segmentar.

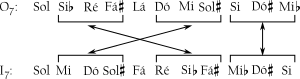
Veja-se como Berg faz uso dessas invariantes compositivamente. Após uma introdução lenta, o violino solo apresenta a figura ascendente mostrada no Exemplo 6-19a, seguida após um breve interlúdio, pela figura descendente mostrada no Exemplo 6-19b. A figura ascendente é O₇ e a descendente é I₇. Note-se que a segunda figura é a inversão de notas bem como a inversão de classes de notas da primeira - os intervalos ordenados de classes de notas simplesmente estão revertidos. As duas (048) trocam de lugar e (024) permanece no mesmo lugar. As duas linhas melódicas estão assim associadas não somente por sua clara relação inversiva, mas pelos seus subconjuntos segmentados compartilhados também. Associações segmentares desse tipo proveem um belo jeito de ouvir um caminho pela da música dodecafônica.

6.4.3 Díades invariantes entre formas da série.

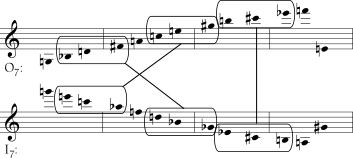
Para um tipo diferente de invariância sob inversão considere-se o que acontce quando uma série soa nota contra nota com uma forma inversivamente relacionada. Usar-se-á a série de Piano Variations, op. 27 de Webern como exemplo, embora a relação discutida seja verdadeira para qualquer par de séries relacionadas por inversão. O Exemplo 6-20 mostra O₈ soando nota contra nota com I₁₀.

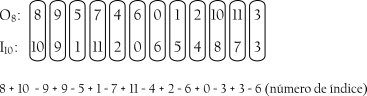
As díades de classes de notas formadas entre as séries são invariantes. Se 8 soa com 10 uma vez, ele soará com 10 outra vez. O 1 soa somente com 5, 2 com 4 e assim por diante. Há somente sete díades de classes de notas diferentes e cada uma delas ocorre duas vezes, exceto para os uníssonos 9 e 3, cada qual ocorrendo uma vez. Para entender porque isso é assim, deve-se pensar em termos de números de índice. O número de índice dessas duas formas da série inversivamente relacionadas é 6. A soma de cada elemento na primeira série com o elemento correspondente na série inversivamente relacionada deve ser 6. Mas não há muitas maneiras diferentes de somar 6. Se há um 7 em uma série, deve haver um 11 correspondente na outra, porque nenhuma outra classe de notas pode ser adicionada a 7 para fazer 6.

Ao se transpor uma das duas séries acima, pode-se ainda manter aquelas díades de classes de notas invariantes desde que se mantenha o número de índice. Por exemplo, ao se transpor O₈ cinco semitons mais agudo para O₁, precisa transpor I₁₉ cinco semitons mais grave para I₅ para manter o número de índice como 6 (Exemplo 6-18).

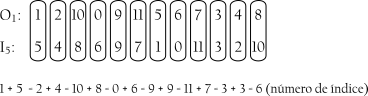
Webern explora essa relação invariante no segundo movimento de Piano Variations, op. 27. O Exemplo 6-19 [*] mostra os primeiros três pares de formas da série: O está sendo emparelhada com uma I de modo que o número de índice permaneça 6 mesmo quando as séries são transpostas.

Como resultado, há somente sete díades de classes de notas diferentes no movimento: Sol-Si, Lá-Lá, Fá-Dó, Sol-Si, Mi-Ré, Fá-Dó e Mi-Mi. Estas sete díades soam repetidamente, dando ao movimento uma unidade que é fácil de ouvir.

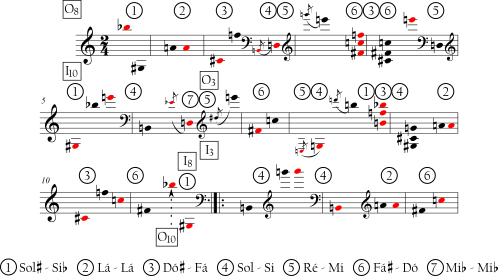
Ao mesmo tempo uma variedade rítmica é provida, já que as díades nem sempre ocorrem na mesma ordem. Assim como com outras relações de invariância, essas díades de classes de notas fixas ajudam a ouvir um caminho pela peça. Como o número de índice permanece constante, as duas séries e todas as díades podem ser ouvidas equilibradas no mesmo eixo, especificamente Lá-Mi. O Lá acima do Dó central é particularmente audível como um centro de nota. Ele é sempre ouvido como um uníssono entre as formas da série e todas as outras notas estão arranjadas simetricamente em torno dele.

O que é importante aqui, assim como em toda música dodecafônica, não é a mera presença da série, mas seu conteúdo musical audível e a cadeia de associações criadas por suas transformações. Ao analisar música dodecafônica, pode ser útil começar pela identificação da série. Mas isso é só o começo. A série não é um objeto estático que é mecanicamente repetido várias e várias vezes, mas uma rica rede de relações musicais que são expressas e desenvolvidas de muitas maneiras.

Uma invariante é qualquer elemento ou relação preservada quando uma série é transformada. Invariantes são importantes fontes de continuidade na música dodecafônica