UNIDADE 5.
Acordes.
Antes de iniciar o estudo desta unidade certifique-se de ter compreendido e estudado o conteúdo da Unidade 2 (intervalos) e principalmente da Unidade 4 (escalas). Acordes são formados por intervalos harmônicos e acordes diatônicos são construídos com os membros de uma determinada escala. Portanto, dificuldades para ler, escrever e entoar intervalos e escalas, tornarão impraticável o estudo dos acordes.
Generalidades.
O sistema tonal baseia-se em apenas dois modos. O modo maior e o modo menor. Este sistema originou-se da lenta redução do sistema modal cujos modos alteravam frequentemente o sexto e o sétimos graus da escala e, portanto, eram basicamente ou modos maiores ou modos menores (ver os itens: graus modais e graus tonais na Unidade 4). Se por um lado essa simplificação eliminou algumas características dos modos, por outro garantiu uma estabilidade funcional que vinha paulatinamente se cristalizando na música de então.
O termo acorde refere-se à superposição de intervalos harmônicos de terça. É preciso haver pelo menos três notas, consequentemente dois intervalos, para se definir com precisão um acorde. Com duas notas apenas, pode-se inferir pelo contexto, qual o acorde envolvido, mas a rigor, duas notas formam apenas um intervalo, não um acorde. Como o sistema tonal é baseado em terças, as unidades mais simples de acordes contêm duas terças superpostas, ou seja, três notas que formam dois intervalos de terça. Há, portanto, um intervalo de terça entre a primeira e a segunda notas e, outro intervalo de terça entre a segunda e a terceira notas. Para classificar os acordes, entretanto, precisa-se considerar o intervalo entre a primeira e a terceira notas, que será sempre um intervalo de quinta, já que a superposição de duas terças forma um intervalo de quinta que, poderá ser diminuta, justa ou aumentada. Assim, há apenas quatro possibilidades de superpor duas terças que, a partir de agora, chamar-se-ão: tríades.
01 - Estrutura geral e classificação das tríades.
Em função da ordem dos intervalos e dos tipos de quintas possíveis, as tríades podem ser classificadas em quatro tipos distintos:
- Tríades diminutas: são obtidas pela superposição de duas terças menores; são caracterizadas pelo intervalo de quinta diminuta - de onde obtém o seu nome - entre a primeira e a terceira notas quando os intervalos estão dispostos em terças superpostas.
- Tríades perfeitas menores: são obtidas pela superposição de uma terça menor e uma terça maior. Atenção: a ordem das terças é importante para determinar a classificação das tríades perfeitas, já que tanto as perfeitas menores quanto as perfeitas maiores são formadas pela superposição de uma terça menor e uma maior ou, ao contrário, de uma maior e outra menor e, em ambos os casos, terão consequentemente a quinta justa. Quem determina se uma tríade perfeita será menor ou maior é a terça mais grave, ou seja, a terça entre a primeira nota e a segunda nota.
- Tríades perfeitas maiores: são obtidas pela superposição de uma terça maior e outra menor; terão obviamente a quinta justa assim como as perfeitas menores. As tríades perfeitas recebem este nome pelo fato de terem a quinta justa ou: perfeita, como seu nome em grego sugere e como ainda hoje é denominada em algumas línguas.
- Tríades aumentadas: são obtidas pela superposição de duas terças maiores; são caracterizadas pelo intervalo de quinta diminuta, daí o seu nome, entre a primeira e a terceira notas.
O Exemplo 1 a seguir mostra de forma esquemática, as quatro possibilidades de superpor terças, seus intervalos resultantes e sua classificação.

Lembre-se: duas terças menores sempre formam uma quinta diminuta; uma terça maior e outra menor ou vice-versa sempre formam uma quinta justa; duas terças maiores sempre formam uma quinta aumentada.
02 - Estrutura geral e classificação das tétrades.
A superposição de mais uma terça sobre as tríades forma acordes de quatro notas que, a partir de agora, chamar-se-ão tétrades. Ainda que haja várias possibilidades de distribuir três terças, apenas cinco são as mais comuns. Como há uma nota a mais, há também mais um intervalo a ser considerado para a classificação das tétrades: o intervalo entre a primeira e a terceira notas que será sempre um intervalo de sétima que, poderá ser diminuta, menor ou maior.
As tétrades alinhadas na primeira linha do Exemplo 2 são as mais comuns e as mais importantes por suas funções harmônicas. As que estão na segunda linha são mais raras e funcionalmente menos relevantes e por isso estão um pouco descoradas. As duas tétrades que estão emolduradas por um tracejado vermelho são especiais e, carecem de mais explicação a seu tempo. As tétrades mostradas no Exemplo 2 são constituídas e classificadas como segue:
- Tétrades perfeitas maiores com sétima maior: obtidas pela superposição de uma terça maior sobre uma tríade perfeita maior;
- Tétrades perfeitas maiores com sétima menor: obtidas pela superposição de uma terça menor sobre uma tríade perfeita maior; são também chamadas de sétima da dominante;
- Tétrades perfeitas menores com sétima menor: obtidas pela superposição de uma terça menor sobre uma tríade perfeita menor;
- Tétrades diminutas com sétima menor: são obtidas pela superposição de uma terça maior sobre uma tríade diminuta; são também denominadas de sétima meio diminuta;
- Tétrades diminutas com sétima diminuta: obtidas pela superposição de uma terça menor sobre uma tríade diminuta;

A tétrade perfeita maior com sétima menor que, como se viu, é também denominada de sétima da dominante é a única tétrade diatônica (sem alterações) que é naturalmente formada por uma tríade perfeita maior com sétima menor; as outras tríades ou são perfeitos maiores com sétima maior ou, são menores com sétima menor. Há outras características importantes nesta tétrade que serão abordadas com mais detalhe posteriormente.
As duas tétrades circundadas pelo tracejado vermelho mencionadas anteriormente são particularmente importantes porque tem funções semelhantes tanto entre si como também com a tétrade da sétima da dominante. Como ambas são construídas sobre uma tríade diminuta, para diferenciar a que tem uma terça maior da que tem uma terça menor sobre a tríade diminuta, a primeira recebe a denominação de meio diminuta, já que a outra, além da quinta diminuta da tríade diminuta tem também a sétima diminuta e, por isso, é também chamada de totalmente diminuta. A tétrade diminuta com sétima diminuta resulta da superposição de três terças menores.
É possível acrescentar mais terças sobre as tétrades. Com quatro terças formam-se pêntades (cinco notas), chamadas de acordes de nona pelo fato de o intervalo entre a primeira e a quinta notas compreende um intervalo de nona; com seis terças tem-se héxades (seis notas), chamadas de acordes de décima primeira, intervalo resultante entre a primeira e a sexta notas e, finalmente, as héptades (sete notas), também ditas acordes de décima terceira, decorrente do intervalo entre a primeira e a sétima notas. Observe-se que as héptades contém todas as sete notas da escala diatônica a partir das quais os acordes são formados. Superposições de mais de sete notas são chamadas de simultaneidades.
03 - Denominação genérica dos membros e identificação das tríades e tétrades.
Quando uma tríade ou uma tétrade (ou qualquer outro acorde) estiver escrita como uma superposição de terças contíguas, a nota mais grave recebe o nome de fundamental. É ela quem dá o nome à tríade ou tétrade e a primeira terça a partir dela define se a tríade ou tétrade é maior ou menor. Como já foi visto anteriormente, se a primeira terça for menor e a quinta for justa, recebe o nome de menor, se for maior e a quinta for justa, recebe o nome de maior. Se a primeira terça for menor e quinta diminuta, será chamada de diminuta. Se a primeira terça for maior e a quinta for aumentada será chamada de aumentada. A primeira terça acima da fundamental recebe o nome de terça e a segunda terça recebe o nome de quinta, por razões óbvias, já que aqueles nomes são os nomes dos intervalos formados por aquelas notas com a fundamental. No caso das tétrades haverá mais um intervalo a considerar e, portanto, a última terça será chamada de sétima. Se houver mais terças, serão chamadas de nona, décima primeira e décima terceira respectivamente, pelas mesmas razões. Observe-se um detalhe interessante: se a fundamental de uma tríade ou tétrade estiver escrita em uma linha, todos os demais membros estarão nas linhas consecutivas e, se estiver escrita em um espaço, todos os demais membros estarão em espaços consecutivos.

04 - Formação das tríades no modo maior.
Para construir as tríades no modo maior, parte-se da escala de Dó maior como modelo para todas as demais tonalidades maiores. O primeiro passo é "estender" (escrever em ordem diatônica) a escala, acrescentar terças acima de cada nota e, depois, mais uma terça acima da anterior (ou uma quinta acima da primeira). Em função da ordem das terças e das quintas resultantes da superposição de duas terças, classificam-se as tríades identificando-as com a seguinte terminologia: numerais romanos com letras maiúsculas identificam tríades perfeitas maiores; numerais romanos com letras minúsculas identificam tríades perfeitas maiores; numerais romanos com letras maiúsculas acrescidas do sinal de "+" identificam as tríades aumentadas e, numerais romanos com letras minúsculas acrescidas do sinal de graus "°" as tríades diminutas. O Exemplo 3 apresenta as tríades classificadas bem como os intervalos que as formam.

Nas tonalidades maiores, sempre as tríades dos primeiro, quarto e quinto graus são perfeitas maiores; as tríades dos segundo, terceiro e sexto graus são perfeitas menores; a tríade do sétimo grau é sempre diminuta.
05 - Formação das tríades no modo menor.
A formação das tríades no modo menor é um pouco mais complexa porque os sexto e sétimo graus da escala podem ser alterados e, portanto, qualquer tríade que contenha essas notas na sua constituição terá duas formas: uma com o sexto e sétimo graus naturais e outra com os sexto e sétimo graus alterados. Isso acontece pelo fato de que as notas da escala menor melódica poderem ser harmonizadas de uma ou outra forma. Como todas as tríades, exceto a tônica, contêm ou o sexto ou o sétimo graus como fundamental, terça ou quinta, haverá duas tríades diferentes para cada um dos outros graus. O Exemplo 5 mostra as tríades possíveis no modo menor. Abreviou-se lá no exemplo o passo-a-passo para formar as tríades, mas o processo é o mesmo daquele para as tríades do modo maior. As tríades mais incomuns de serem encontradas estão mostradas com uma coloração esmaecida. Atenção: a construção das tríades típicas do modo menor parte sempre da escala menor natural, com alterações do sétimo grau apenas na tríade do quinto grau (dominante) e do sétimo grau sensível.
Há duas abordagens para demonstrar a formação das tríades no modo menor: uma é construindo as tríades com a escala natural da tonalidade relativa (tem a mesma armadura de clave, porém, tônicas diferentes, por exemplo: Dó maior e Lá menor) ou, partindo da escala natural da tonalidade homônima (têm a mesma tônica, mas armaduras de clave diferentes, por exemplo: Dó maior e Dó menor). As duas tem pontos positivos e, portanto, veremos as duas, iniciando com a escala relativa para mostrar que as tríades são as mesmas, com exceção das tríades do quinto e do sétimo graus.
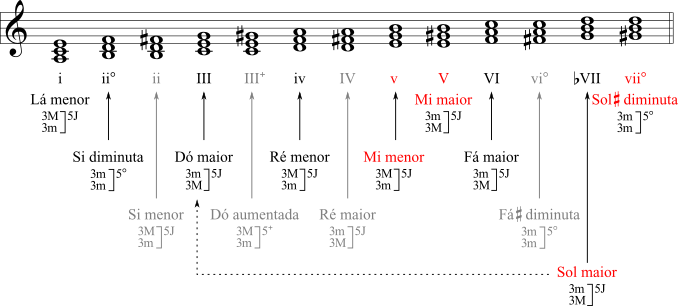
O sexto grau da escala de Lá menor é a nota Fá natural que na forma ascendente da escala menor melódica de Lá menor pode ser alterada para Fá sustenido, para evitar o salto de segunda aumentada entre o sexto grau natural e o sétimo grau sensível. Assim, a tríade do segundo grau de Lá menor terá uma forma com o Fá natural e outra com o Fá sustenido. O que caracteriza o segundo grau no modo menor é a primeira forma, a tríade de Si diminuta, que não contém alterações e, portanto, é nativa do modo, diferente da forma com o Fá sustenido que, sendo uma tríade perfeita menor, caracteriza o modo maior (esta forma estaria presente como segundo grau na tonalidade de La maior). Assim, normalmente considera-se o segundo grau com a tríade diminuta como o padrão, mas encontra-se também a forma com o Fá sustenido quando se quer harmonizar esta nota com a tríade do segundo grau.
Semelhantemente, a tríade do terceiro grau contém o sétimo grau da escala como quinta e, portanto, também terá duas formas: uma com o Sol natural e outra com o Sol sustenido. A tríade perfeita maior do terceiro grau é o mais das vezes o padrão para o modo menor, já que é a tríade relativa e não tem alterações. A forma com o Sol sustenido, que transforma a tríade perfeita maior em uma tríade aumentada, torna esta tríade bastante instável harmonicamente e geralmente é percebida como um acorde de passagem.
A tríade do quarto grau, a subdominante, tem o sexto grau da escala como terça e, portanto, terá duas formas: uma com o Fá natural e outra com o Fá sustenido. A tríade perfeita menor é a que caracteriza o modo menor, já a tríade maior, com o Fá sustenido, é típica do modo maior e só é usada quando se quer harmonizar o sexto grau alterado da escala menor melódica na forma ascendente com a tríade do quarto grau.
A tríade do quinto grau tem o sétimo grau da escala como terça e, como já se viu, terá duas formas: uma com o Sol natural e outra com o Sol sustenido. Aqui é importante observar que as duas formas são frequentemente encontradas, mas com funções harmônicas diferentes. Este tópico será abordado mais adiante. Por ora, basta ressaltar que a tríade perfeita menor (no caso: Mi menor) é a dominante modal e a tríade perfeita maior (Mi maior) é a dominante tonal, pois contém o Sol sustenido como terça que e a sensível, o sétimo grau da escala e, portanto, exerce maior atração sobre a tônica do que a forma com o Sol natural (subtônica). Importante: a força atrativa que provoca tensão harmônica no sistema tonal é o semitom. Assim, grosso modo, enquanto não se ouvir um Sol sustenido, não se tem certeza de se estar em Dó maior ou em La menor, mas assim que o Sol sustenido for ouvido, imediatamente ouvir-se-á o Lá como tônica devido á atração do semitom que há entre o Sol sustenido e o Lá. A passagem do sistema modal para o tonal se dá justamente pela substituição do sétimo grau subtônica pelo sétimo grau sensível, particularmente nas cadências finais.
Analogamente, a tríade do sexto grau agora tem o sexto grau da escala como fundamental e, consequentemente, duas formas: uma com o Fá natural e outra com o Fá sustenido. A forma com o Fá natural é a que caracteriza o modo menor enquanto a forma com o Fá sustenido resulta em uma tríade diminuta, incomumente encontrada como fundamental da tríade do sexto grau.
Finalmente, a tríade do sétimo grau tem o sétimo grau da escala como fundamental resultando em duas formas: uma com o Sol natural e outra com o Sol sustenido. Aqui, novamente, entre em cena o sétimo grau como subtônica e como sensível. A tríade do sétimo grau com o Sol natural é característica da música modal, mas tem outra função harmônica tonal extremamente importante: ela será ouvida como a tríade da dominante da tonalidade relativa, no caso: a tríade de Sol maior será ouvida como dominante de Dó maior e, portanto, não se ouvirá o Lá como tônica e sim o Dó. Importante: o que caracteriza a tonalidade de Lá menor é a tríade diminuta do sétimo grau, que contém a sensível como fundamental.Nas tonalidades menores com as tríades características, sempre as tríades dos primeiro e quarto graus são perfeitas menores; as tríades dos terceiro e sexto graus são perfeitas maiores; as tríades dos segundo e sétimo graus são diminutas.
06 - Comparação entre as tríades no modo maior com as do menor.
Viu-se que a formação das tríades no modo menor pode ser mostrada com a tonalidade relativa ou com a homônima. No Exemplo 6a a seguir pode-se comparar as duas formas. Com a tonalidade relativa, pode-se verificar mais facilmente que tríades da tonalidade relativa são os mesmos da tonalidade original com exceção de duas: a tríade da dominante (cuja terça é o sétimo grau sensível)e a própria tríade diminuta da sensível que, são justamente as tríades que definem a tonalidade relativa por conterem o sétimo grau sensível (alterado) em vez do sétimo grau subtônica que é nativo da escala natural menor. Observe-se que a tônica da tonalidade relativa menor é o sexto grau da escala maior ou, mais por estar mais perto, uma terça menor abaixo da tônica do modo maior (a inversão da sexta é a terça). Por exemplo, o sexto grau da escala de Dó maior é Lá que será a tônica da tonalidade relativa. No Exemplo 6a estão marcadas com setas a rotação das tríades: a tríade da tônica do modo maior será a tríade do terceiro grau da tonalidade relativa menor e, portanto, sua relativa maior; a tríade do segundo grau será a tríade do quarto grau da relativa menor; a tríade do terceiro terá que ser alterada pois no modo maior é uma tríade menor que deverá ser modificada para ficar maior, consequentemente, ao fazer isso, a terça desta tríade que agora está como quinto grau (a dominante) conterá a sensível; a tríade do quarto grau será a a tríade do sexto grau e a tríade; a tríade so quinto grau será também alterada por conter a sensível como fundamental; e tríade do sexto grau será a tônica da relativa menor como já se viu e finalmente, a tríade diminuta do sétimo grau será a tríade do segundo grau que, caracteristicamente e, por esta razão, também é diminuta.
Mais uma observação: toda tonalidade maior tém sua relativa menor e vice-versa. A tônica de uma estará uma terça abaixo da outra no caso da relativa menor e, uma terça acima no caso da relativa maior. Por exemplo: a tônica relativa de Dó maior é Lá menor (terça menor abaixo) e a tônica relativa de Lá menor é Dó maior, (terça menor acima).

Entretanto, para comparar melhor a qualidade das tríades entre os modos maior e menor, torna-se mais fácil comparar as tríades com a tonalidade homônima, já que todas terão as mesmas fundamentais, como se pode ver no Exemplo 6b.

Observe que nas tonalidades homônimas, o acorde da dominante é o mesmo para ambas. As tríades que são maiores no modo maior tornam-se menores no modo menor e, contrariamente, as tríades menores tornam-se maiores, as diminutas continuam diminutas, com exceção da tríade do segundo grau que é menor no modo maior e diminuta no modo menor.
07 - Formação das tétrades no modo maior.
Superpondo-se mais uma terça no topo das tríades obtêm-se as tétrades ou, acordes de sétima. No modo maior, os acordes maiores têm a sétima maior, exceto o acorde de sétima da dominante que é maior, mas com a sétima menor e, os acordes menores têm a sétima menor. Não é preciso indicar se a sétima é maior ou menor, pois sabe-se que somente as tétrades do primeiro e do quarto graus têm a sétima maior e a sétima da dominante é menor, assim como as demais. Importante: a tétrade da dominante com sétima é a única tétrade diatônica e esse fato tem implicações importantes para o sistema tonal como se verá mais adiante.
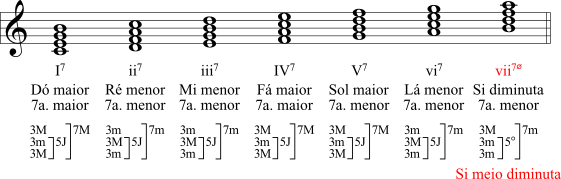
Note-se que a tétrade do sétimo grau é uma tríade diminuta com a sétima menor que é denominada de tétrade meio diminuta, para diferenciar da tétrade do sétimo grau do modo menor que é uma tríade diminuta com a sétima também diminuta.
08 - Formação das tétrades no modo menor.
As considerações sobre as tétrades no modo maior são as mesmas para o modo menor, com exceção da tétrade do sétimo grau que e uma tríade diminuta com uma sétima também diminuta que caracteriza o modo menor. Observe-se a diferença na notação da tétrade do segundo grau (tétrade meio diminuta) e da tétrade do sétimo grau (sétima diminuta).

Importante: Quando se superpõe uma terça maior sobre uma tríade diminuta ele torna-se meio diminuta (a sétima é menor); quando se superpõe uma terça menor sobre uma tríade diminuta ela torna-se totalmente diminuta, como se costuma dizer, ou seja, a quinta pe diminuta e a sétima também é diminuta.
09 - Inversão de tríades.
Assim como os intervalos, os acordes podem ser invertidos. As tríades podem ser encontradas na posição fundamental, primeira inversão e segunda inversão. Quando a tríade está disposta como uma "pilha" de terças, diz-se que ela está na posição fundamental (como foi visto no item 3 acima) e daqui em diante será abreviada como PF. Quando a terça está no baixo, diz-se que está em primeira inversão e, quando a quinta está no baixo, diz-se que está em segunda inversão. Atenção: A expressão "está no baixo" significa que está na posição mais grave, não necessariamente na "voz do baixo".
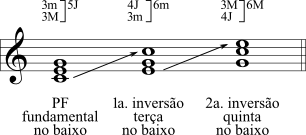
10 - Inversão de tétrades.
As tétrades também podem ser invertidas e, por terem uma terça a mais, terão uma inversão a mais. Semelhantemente às tríades, quando a tétrade está disposta como uma pilha de terças, diz-se que está em posição fundamental (PF), em primeira inversão quando a terça está no baixo, em segunda inversao quando a quinta está no baixo e, em terceira posição quando a sétima está no baixo.

11 - Baixo cifrado.
Para indicar qual a inversão de uma tríade ou tétrade (ou qualquer outro acorde), usa-se um sistema que foi idealizado no início do período Barroco, que era usado para indicar aos instrumentistas de instrumentos harmônicos, quais acordes deveriam ser tocados, pois a parte deles só continha o baixo com alguns números acoplados, ou cifras, indicando ao instrumentísta a que membro do acorde aquela nota escrita pertencia. Daí o termo "baixo cifrado". Com algumas poucas modificação, aquele sistema é até hoje utilizado para indicar as inversões dos acordes. O Quadro 1 a seguir foi modificado a partir de Kostka (2013, p. 44).
| Tríades | |||
|---|---|---|---|
 |  |  |  |
| cifra completa | 5 3 | 6 3 | 6 4 |
| cifra usual | 6 | 6 4 | |
| achar a fundamental | está no baixo | está uma sexta acima do baixo | está uma quarta acima do baixo |
| Tétrades | ||||
|---|---|---|---|---|
 |  |  |  |  |
| cifra completa | 7 5 3 | 6 5 3 | 6 4 3 | 6 4 2 |
| cifra usual | 7 | 6 5 | 4 3 | 4 2 ou 2 só |
| achar a fundamental | está no baixo | está uma sexta acima do baixo | está uma quarta acima do baixo | está uma segunda acima do baixo |
| Outros sinais | ||
|---|---|---|
| Um número seguido por uma alteração indica que aquele intervalo representado pelo número deve ser alterado. | 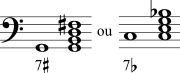 | |
| Uma alteração sozinha refere-se sempre à terça acima da nota do baixo. | 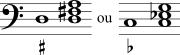 | |
| Um número com um sinal de + acoplado ou cortado por um traço indica que aquela nota deve ser alterada ascendentemente. |  | |
| Um traço indica que a nota ou a base do acorde deve ser mantida ou repetida. |  | |
.
Fim da Unidade 5 (Acordes).
Voltar para as Unidades