UNIDADE 2.
Intervalos
Generalidades.
Nesta unidade estuda-se a parte da notação musical que está relacionada com o tom, o som das notas musicais. Base para o estudo de escalas e da harmonia, importante e fundamental para o solfejo e o ditado, talvez seja a parte mais demorada de dominar. Requer o desenvolvimento de habilidades relacionadas com a audição interna.
01 - Intervalo.
É a diferença medida em semitons entre duas notas (entre o tom, o som das notas).
02 - Intervalos melódicos e harmônicos.
- Melódicos: quando as notas são emitidas em sucessão, ou seja, uma depois da outra.
- Harmônicos: quando as notas são emitidas simultaneamente, ou seja, ao mesmo tempo.

03 - Intervalos simples e compostos.
Já se viu na Unidade 1a o conceito de oitava, por exemplo, quando se estudou os registros, viu-se que Dó4 e Dó5 estão separados por uma oitava. Este conceito é importante para compreender a classificação dos intervalos em simples e compostos.
- Simples: quando as notas estão compreendidas na extensão de uma oitava, incluindo a oitava.
- Compostos: quando as notas ultrapassam a extensão de uma oitava.

04 - Intervalos melódicos ascendentes e descendentes.
Os intervalos melódicos podem ainda ser classificados com ascendentes ou descendentes. Ascendentes quando a primeira nota é mais grave do que a segunda e descendentes quando a primeira nota é mais aguda do que a segunda. Para os intervalos harmônicos não faz sentido usar esta terminologia, pois as duas notas soam simultaneamente.

05 - Classificação dos intervalos.
De acordo com a quantidade de semitons e tons que contém, os intervalos podem ser nomeados conforme o Quadro a seguir. Há sempre dois atributos a serem considerados: o nome do intervalo que é contado entre a primeira e a segunda notas seguindo a ordem natural e a qualificação que diferencia intervalos com o mesmo nime, mas quantidades diferentes de semitons e tons. Os intervalos de primeira, quarta, quinta e oitava podem ser justos (ou perfeitos), aumentados ou diminutos. Os intervalos de segunda, terça, sexta e sétima podem ser maiores, menores, aumentados ou diminutos.
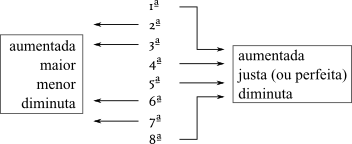
O Quadro a seguir apresenta os intervalos mais utilizados e alguns que são apenas teóricos. Há outros teoricamente possíveis, mas que não são usados que serão vistos mais adiante. No Quadro os intervalos estão indicados por sinais convencionais. O intervalo diminuto será representado por º, o menor por m, o maior por M, o justo por J e o aumentado por +. Os intervalos de primeira, quarta, quinta e oitava estão separados por razões didáticas dos outros pelo fato de serem justos e não admitirem a distinção entre maior e menor. Como a soma de dois semitons formam um tom inteiro, ao lado da quantidade de semitons pode-se ver a quantidade de tons entre parênteses para facilitar a contagem.
| Nome | Quantidade de semitons | Quantidade de semitons | |||||
|---|---|---|---|---|---|---|---|
| º | m | M | + | º | J | + | |
| primeira | -1 (*) | 0 | 1 | ||||
| segunda | 0 | 1 | 2 (1) | 3 (1 ½) | |||
| terça | 2 (1) | 3 (1 ½) | 4 (2) | 5 (2 ½) | |||
| quarta | 4 (2) | 5 (2 ½) | 6 (3) | ||||
| quinta | 6 (3) | 7 (3 ½) | 8 (4) | ||||
| sexta | 7 (3 ½) | 8 (4) | 9 (4 ½) | 10 (5) | |||
| sétima | 9 (4 ½) | 10 (5) | 11 (5 ½) | 12 (6) | |||
| oitava | 11 (5 ½) | 12 (6) | 13 (6 ½) (*) | ||||
(*) Teoricamente possíveis, mas a primeira diminuta suporia um espaço negativo, na verdade, um intervalo composto ao contrário. Já a oitava aumentada, embora classificada como intervalo simples é na verdade um intervalo composto em termos de som, pois soa como a nona menor.
Uma coisa é o nome do intervalo, outra é o tom (o som) do intervalo. Muitos dos intervalos do Quadro anterior tem nomes diferentes, mas a mesma quantidade de semitons e, portanto, tem o mesmo som. Mais adiante em outro Quadro mostra-se-á exemplos.
06 - Semitom diatônico e cromático.
No Quadro 1 pode-se observar que os intervalos de primeira aumentada e segunda menor tem ambos um semitom. Essa diferenciação deve-se ao fato de que há duas possibilidades de obter esses intervalos.
- Semitom diatônico: quando o semitom é formado por duas notas de nomes diferentes. Existe na escala natural entre as notas Mi e Fá e, entre as notas Si e Dó.
- Semitom cromático: quando o semitom é formado por duas notas de nomes iguais, mas com sons diferentes. Sempre haverá um acidente envolvido na formação deste intervalo.
No sistema de afinação de temperamento igual que se usa hoje em dia, em que a oitava é dividida em partes iguais, esses dois semitons são iguais, tem o mesmo som, pois o Ré bemol é enarmônico do Dó sustenido conforme foi visto na Unidade 1a. Mais adiante será explicado que na origem esses semitons eram diferentes.

07 - Formação do intervalo de tom.
O intervalo de um tom inteiro é formado por dois semitons, sendo um diatônico e o outro cromático.

08 - Intervalos simples
No Quadro 2 a seguir estão exemplos dos intervalos a partir da mesma nota. Estudar o Quadro 2 observando os intervalos enarmônicos trará benefícios importantes para o treinamento da leitura musical e, mais ainda, se praticados, quer cantando ou tocando, para o solfejo e o ditado musical.
| Segunda diminuta teórica apenas |  |  | |
 |  |  |  |
 |  |  |  |
 |  |  | |
 |  |  | |
 |  |  |  |
 |  |  |  |
 |  | Oitava aumentada teórica apenas |
Atenção! Intervalos aumentados aos quais se aplica mais um semitom tornam-se superaumentados (ou mais do que aumentados) e intervalos diminutos dos quais se retira um semitom tornam-se subdiminutos (ou mais do que diminutos). Ver o Exemplo 7 a seguir.

Na Unidade 6 (Solfejos) há arquivos de áudio para praticar a entoação e reconhecimento dos intervalos.
09 - Intervalos harmônicos
No Quadro 3 estão mostrados os intervalos harmônicos simples com a nota mais grave sempre fixa na segunda coluna e com a nota mais aguda sempre fixa na terceira coluna.
| Primeira justa | 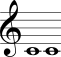 | 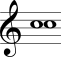 |
| Segunda menor | 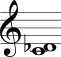 |  |
| Segunda maior | 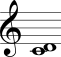 | 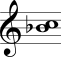 |
| Terça menor |  |  |
| Terça maior | 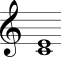 | 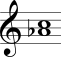 |
| Quarta justa |  | 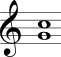 |
| Quarta aumentada Quinta diminuta | 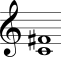 | 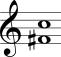 |
| Quinta justa |  |  |
| Sexta menor | 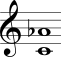 | 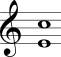 |
| Sexta maior | 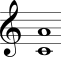 | 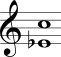 |
| Sétima menor | 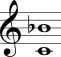 | 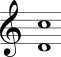 |
| Sétima maior |  | 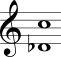 |
| Oitava justa | 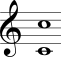 | 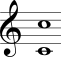 |
Na Unidade 6 (Solfejos) há arquivos de áudio para praticar a entoação e reconhecimento dos intervalos.
10 - Intervalos compostos
Os intervalos tanto melódicos quanto harmônicos que ultrapassam uma oitava são classificados como compostos. No quadro a seguir estão as relações com os seus euivalentes dentro da oitava.
| Nona menor |  | Nona maior |  |
| Décima menor |  | Décima maior |  |
| Décima primeira justa |  | Décima primeira aumentada |  |
| Décima segunda diminuta |  | Décima segunda justa |  |
| Décima terceira menor |  | Décima terceira maior | 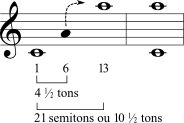 |
| Décima quarta menor |  | Décima quarta maior | 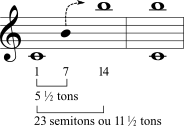 |
| Décima quinta diminuta |  | Décima quinta justa |  |
| * observar a diferença na formação do trítono na 11a. aumentada e na 11a. diminuta; ** a 15a. diminuta é enarmônica da 14. maior. |
|||
Intervalos que ultrapassam a 15a. (duas oitavas) teoricamente podem ser classificados com 16a., 17a. etc., mas em geral são reduzidos à intervalos simples com a quantidade de oitavas envolvidas, por exemplo: terça menor mais três oitavas.
11 - Intervalos naturais
A escala natural é uma sucessão de tons e semitons diatônicos sem alterações (corresponde às teclas brancas do piano). Os intervalos naturais entre todas as suas notas estão sintetizados no Exemplo 8 a seguir.

Considerando esses intervalos no âmbito de uma oitava tem-se diferentes quantidades de cada tipo de intervalo. Ver o Quadro 5 a seguir.
| Intervalo | Quantidade |
|---|---|
| Segundas | 7 (duas menores e cinco maiores) |
| Terças (*) | 6 (três menores e três maiores) |
| Quartas | 5 (quatro justas e uma aumentada) |
| Quintas | 4 (quatro justas) |
| Sextas (*) | 3 (uma menor e duas maiores) |
| Sétimas | 2 (uma menor e uma maior) |
| Oitavas | 1 (uma justa) |
Nas terças, as que contém um semitom em sua composição são menores e as que não o tem são maiores; nas sextas, as que contêm dois semitons são menores e as que contém apenas um são maiores.
12 - Inversão de intervalos
A inversão de um intervalo resulta de uma operação em que se transporta a nota mais grave uma oitava acima (ou a nota mais aguda uma oitava abaixo). Somente intervalos simples podem ser invertidos, uma vez que os intervalos compostos quando invertidos tornam-se intervalos simples. A aplicação da operação de inversão observa as seguintes propriedades: a primeira inverte-se na oitava e vice-versa; a segunda inverte-se na sétima e vice-versa; a terça na sexta e vice-versa e assim por diante. Também os intervalos maiores invertem-se em menores e vice-versa, os justos permanecem justos e os diminutos invertem-se em aumentados e vice-versa.
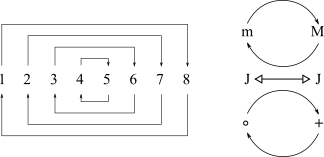
Teoricamente há muitos outros intervalos que também podem ser invertidos - por exemplo: a segunda diminuta Dó - Ré dobrado bemol, mas esse intervalo é enarmònicco da primeira justa (ou uníssono). No Quadro 6 estão apresentadas apenas as inversões mais comuns. A inversão de intervalos é um conceito muito importante para o estudo de harmonia e, portanto, todo esforço em compreender este tópico deve ser empreendido.
| Intervalos melódicos ascendentes e descendentes | Intervalos harmônicos |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
13 - Intervalos consonantes e dissonantes
O termo consonante significa literalmente "que soa junto", com sentido de concordante e, o termo dissonante traz a ideia de que discorda, destoa. A classificação de intervalos em consonantes e dissonantes varia conforme o período histórico. Na teoria musical considera-se em princípio: os intervalos justos: uníssono, quarta, quinta e oitava como consonâncias perfeitas; as terças e sextas menores e maiores como consonâncias imperfeitas; segundas e sétimas menores e maiores e, os intervalos aumentados e diminutos como dissonantes. A quarta é considerada consonante, entretanto, na teoria da música modal, a quarta quando formada com o baixo (a nota mais grave), é considerada uma dissonância.
Fim da Unidade de Intervalos.
Voltar para as Unidades